Lời giải chi tiết:

Ta có: \(f'\left( x \right) = {x^2} - 2\left( {m + 1} \right)x - \left( {2m - 1} \right)\)

Cho \(f'\left( x \right) = 0 \Leftrightarrow {x^2} - 2\left( {m + 1} \right)x - \left( {2m - 1} \right) = 0\)

+ Theo Viet ta có \(\left\{ \begin{array}{l}{x_1}{x_2} =  - \left( {2m - 1} \right)\\{x_1} + {x_2} = 2\left( {m + 1} \right)\end{array} \right.\)

+ Để hàm số có 2 điểm cực trị \( \Rightarrow f'\left( x \right) = 0\) phải có 2 nghiệm phân biệt

\( \Rightarrow \Delta  > 0 \Leftrightarrow 4{\left( {m + 1} \right)^2} + 4\left( {2m - 1} \right) > 0 \Leftrightarrow 4{m^2} + 16m > 0 \Leftrightarrow \left[ \begin{array}{l}m <  - 4\\m > 0\end{array} \right.\)

+ Có: \(T = x_1^2 + x_2^2 - 10\left( {{x_1} + {x_2}} \right) = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 10\left( {{x_1} + {x_2}} \right)\)

            \( = 4{\left( {m + 1} \right)^2} + 2\left( {2m - 1} \right) - 20\left( {m + 1} \right) = 4{m^2} - 8m - 18\)

YCBT tìm \({T_{\min }} \Leftrightarrow \) tìm GTNN của \(y = 4{m^2} - 8m - 18\)

+ Xét \(y = 4{m^2} - 8m - 18\)

TXĐ: \(D = \left( { - \infty  - 4} \right) \cup \left( {0; + \infty } \right)\)  

\(y' = 8m - 8 = 0 \Rightarrow m = 1\)

BBT:

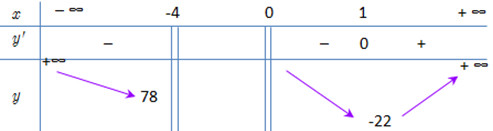
Dựa vào bảng biến thiên, giá trị nhỏ nhất của \(T =  - 22\) khi \(m=1.\)

Chọn D.