Lời giải chi tiết:

Tập xác định: \(D = \left( { - \infty ;4} \right]\)

Ta có

\(\begin{array}{l}y' = \sqrt {4 - x}  - \dfrac{x}{{2\sqrt {4 - x} }} = \dfrac{{2\left( {4 - x} \right) - x}}{{2\sqrt {4 - x} }} = \dfrac{{8 - 3x}}{{2\sqrt {4 - x} }}\,\,\,\left( {x \ne 4} \right)\\y' = 0 \Leftrightarrow x = \dfrac{8}{3}\,\,\,\,\left( {tm} \right)\end{array}\)

Ta có bảng biến thiên:

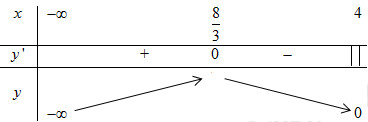
Dựa vào bảng biến thiên, hàm số nghịch biến trên \(\left( {\dfrac{8}{3};4} \right).\)

Chọn A.