Phương pháp giải:

B1: Lập BBT của hàm số trên đoạn cần tìm.

B2: Từ BBT, ta tìm giá trị \(m\) thoả mãn yêu cầu bài toán.

Lời giải chi tiết:

Hoành độ đỉnh của parabol \(y = {x^2} - 2x + 2m + 3\) là \({x_I} = \frac{2}{2} = 1 \Rightarrow {y_I} = 2m + 2.\)

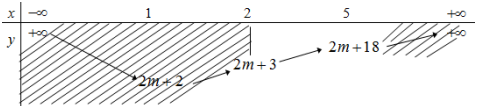
Ta có BBT của hàm số \(y = {x^2} - 2x + 2m + 3\) trên đoạn \(\left[ {2;5} \right]\)

Từ BBT, ta thấy giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ {2;5} \right]\) của hàm số \(y = {x^2} - 2x + 2m + 3\) là  \(M = 2m + 3.\)

Theo giả thiết ta có: \(2m + 3 =  - 3 \Leftrightarrow 2m =  - 6 \Leftrightarrow m =  - 3.\)

Chọn A.