Câu hỏi
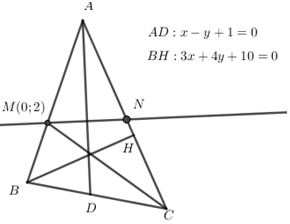
Trong mặt phẳng với hệ toạ độ \(Oxy,\) cho tam giác ABC có đường cao \(BH:3x + 4y + 10 = 0\), đường phân giác trong góc \(A\) là \(AD\) có phương trình \(x - y + 1 = 0,\) điểm \(M\left( {0;2} \right)\) thuộc đường thẳng AB đồng thời cách C một khoảng bằng \(\sqrt 2 .\) Tìm toạ độ các đỉnh của tam giác \(ABC\) biết toạ độ điểm \(C\) là các số nguyên.
- A \(A\left( {5;6} \right);B\left( { - 3; - \frac{1}{4}} \right);C\left( {1;1} \right)\)
- B \(A\left( {4;5} \right);B\left( { - 3; - \frac{1}{4}} \right);C\left( {1;1} \right)\)
- C \(A\left( {5;6} \right);B\left( {3; - \frac{1}{4}} \right);C\left( {1;1} \right)\)
- D \(A\left( {4;5} \right);B\left( {3; - \frac{1}{4}} \right);C\left( { - 1;1} \right)\)
Phương pháp giải:
Sử dụng tính chất đường phân giác trong của tam giác để làm bài toán.
Lời giải chi tiết:
Gọi \(N\) là điểm đối xứng với \(M\) qua \(AD.\)
\(AC\) là đường thẳng đi qua \(N\left( {1;\,\,1} \right)\) và vuông góc với \(BH:\,\,\,3x + 4y + 10 = 0\)
\( \Rightarrow AC:\,\,4\left( {x - 1} \right) - 3\left( {y - 1} \right) = 0 \Leftrightarrow 4x - 3y - 1 = 0.\)
Ta có: \(AD \cap AC = \left\{ A \right\} \Rightarrow \) tọa độ điểm \(A\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}4x - 3y - 1 = 0\\x - y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 5\end{array} \right. \Rightarrow A\left( {4;\,\,5} \right).\)
Phương trình đường thẳng \(AB\) đi qua \(A\left( {4;\,\,5} \right)\) và \(M\left( {0;\,\,2} \right)\) là:
\(\frac{{x - 4}}{{0 - 4}} = \frac{{y - 5}}{{2 - 5}} \Leftrightarrow 3x - 12 = 4y - 20 \Leftrightarrow 3x - 4y + 8 = 0.\)
Có \(BH \cap AB = \left\{ B \right\} \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}3x - 4y + 8 = 0\\3x + 4y + 10 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - \frac{1}{4}\end{array} \right. \Rightarrow B\left( { - 3;\, - \frac{1}{4}} \right).\)
Gọi \(C \in AC:\,\,\,4x - 3y - 1 = 0 \Rightarrow C\left( {c;\,\,\frac{{4c - 1}}{3}} \right)\,\,\,\,\,\left( {c \in \mathbb{Z}} \right).\)
Ta có \(MC = \sqrt 2 \Leftrightarrow M{C^2} = 2\)
\(\begin{array}{l} \Leftrightarrow {\left( {0 - c} \right)^2} + {\left( {2 - \frac{{4c - 1}}{3}} \right)^2} = 2 \Leftrightarrow {c^2} + {\left( {\frac{7}{3} - \frac{{4c}}{3}} \right)^2} = 2\\ \Leftrightarrow \frac{{25}}{9}{c^2} - \frac{{56}}{9}c + \frac{{31}}{9} = 0\\ \Leftrightarrow \left[ \begin{array}{l}c = 1\,\,\,\left( {tm} \right)\\c = \frac{{31}}{{25}}\,\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow C\left( {1;\,\,1} \right).\end{array}\)
Kiểm tra điều kiện B, C khác phía với AD, ta có hai điểm đều thoả mãn.
Chọn B