Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên\(SA \bot \left( {ABCD} \right)\) và \(SA = a\). Khoảng cách giữa hai đường thẳng \(SB\) và \(AD\) là:
- A \(a\sqrt 2 \)
- B \(\dfrac{{a\sqrt 2 }}{2}\)
- C \(\dfrac{{a\sqrt 2 }}{3}\)
- D \(\dfrac{{a\sqrt 3 }}{2}\)
Lời giải chi tiết:
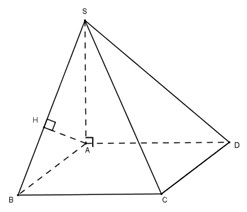
Trong (SAB) kẻ \(AH \bot SB\) ta có:
\(\left. \begin{array}{l}AD \bot AB\\AD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow AD \bot AH\)
\( \Rightarrow AH\) là đoạn vuông góc chung của SB và AD\( \Rightarrow d\left( {SB;AD} \right) = AH\)
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB \Rightarrow \Delta SAB\)vuông tại A.
\( \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{2}{{{a^2}}} \Rightarrow AH = \dfrac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {SB;AD} \right) = \dfrac{{a\sqrt 2 }}{2}\)
Chọn B.







