Phương pháp giải:

Sử dụng phương pháp dựng khoảng cách từ chân đường vuông góc dến một mặt phẳng.

Lời giải chi tiết:

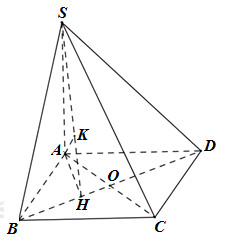
Trong (SBD) kẻ \(SH \bot BD\), trong (SAH) kẻ \(AK \bot SH\)

Ta có: \(\left. \begin{array}{l}BD \bot SH\\BD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow BD \bot \left( {SAH} \right) \Rightarrow BD \bot AK\)

Có: \(\left. \begin{array}{l}AK \bot BD\\AK \bot SH\end{array} \right\} \Rightarrow AK \bot \left( {SBD} \right) \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AK\)

Xét tam giác vuông ABD có: \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}}\)

Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AH \Rightarrow \Delta SHA\) vuông tại A.

\( \Rightarrow \dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{S{A^2}}} = \dfrac{5}{{4{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{9}{{4{a^2}}} \Rightarrow AK = \dfrac{{2a}}{3}\)  

Chọn B.