Câu hỏi
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật dài 12cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ)? Gọi O1 là tâm cuả hình chữ nhật; O2 là tâm của hình vuông.
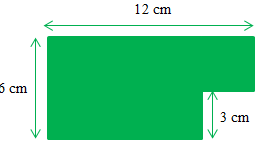
- A Trọng tâm G nằm trên đường nối O1 và O2 và cách O1 một đoạn 0,88cm
- B Trọng tâm G nằm trên đường nối O1 và O2 và cách O1 một đoạn 5,3cm
- C Trọng tâm G nằm trên đường vuông góc với đường thẳng nối O1 và O2 và cách O1 một đoạn 0,88cm
- D Trọng tâm G nằm trên đường vuông góc với đường thẳng nối O1 và O2 và cách O1 một đoạn 5,3cm
Phương pháp giải:
Quy tắc tổng hợp hai lực song song cùng chiều:
- Hợp lực của hai lực song song cùng chiều là một lực song song, cùng chiều và có độ lớn bằng tổng các độ lớn của hai lực ấy.
- Giá của hợp lực chia khoảng cách giữa hai giá của hai lực song song thành những đoạn tỉ lệ nghịch với độ lớn của hai lực ấy.
\(F = {F_1} + {F_2};\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{d_2}}}{{{d_1}}}\) (chia trong)
Lời giải chi tiết:
Hình vẽ biểu diễn lực:
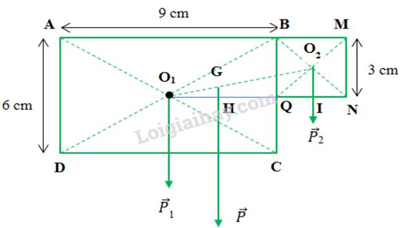
Chia bản mỏng thành hai phần: ABCD và BMNQ. Trọng tâm của 2 phần này là O1 và O2. Nếu gọi trọng tâm của bản là G thì G sẽ là điểm đặt của hợp lực của các trọng lực P1 và P2 của hai bản nói trên.
Do các bản phẳng mỏng, đồng chất nên trọng lượng của mỗi tấm tỉ lệ với diện tích.
Ta có: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{6.9}}{{3.3}} = 6\)
Khi đó G được xác định như sau: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{HI}}{{H{O_1}}} = \dfrac{{G{O_2}}}{{G{O_1}}} = 6 \Rightarrow G{O_2} = 6.G{O_1}\,\,\,\,\,\,\,\left( 1 \right)\)
Mặt khác ta có:
\(\begin{array}{l}
G{O_1} + G{O_2} = {O_1}{O_2} = \sqrt {{O_1}{I^2} + {O_2}{I^2}} = \sqrt {{{\left( {4,5 + 1,5} \right)}^2} + {{1,5}^2}} = 6,18cm\\
\Rightarrow G{O_1} + G{O_2} = 6,18cm{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)
\end{array}\)
Từ (1) và (2) → GO1 = 0,88 cm
Vậy trọng tâm G nằm trên đường nối O1 và O2 và cách O1 một đoạn 0,88cm.
Chọn A







