Lời giải chi tiết:

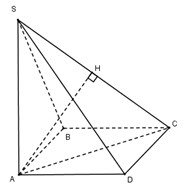
\(\widehat {BAD} = {60^0} \Rightarrow \widehat {ABC} = {120^0}\)

Áp dụng định lí Côsin trong tam giác ABC ta có:

\(AC = \sqrt {A{B^2} + B{C^2} - 2AB.BC.c{\rm{os}}\widehat {ABC}} \)\( = \sqrt {{a^2} + {a^2} - 2{a^2}\left( { - \dfrac{1}{2}} \right)}  = a\sqrt 3 \)  

\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC\)\( \Rightarrow \Delta SAC\)  vuông tại A

Áp dụng hệ thức lượng trong tam giác vuông SAC ta có:

\(\begin{array}{l}\,\,\,\,\,\,\dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{A{H^2}}}\\ \Rightarrow \dfrac{1}{{S{A^2}}} = \dfrac{1}{{A{H^2}}} - \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{a^2}}} - \dfrac{1}{{3{a^2}}} = \dfrac{2}{{3{a^2}}}\\ \Rightarrow SA = \dfrac{{a\sqrt 6 }}{2}\end{array}\)

\(\begin{array}{l}{S_{\Delta ABC}} = \dfrac{1}{2}AB.BC.\sin \widehat {ABC} = \dfrac{1}{2}{a^2}\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4}\\ \Rightarrow {S_{ABCD}} = 2{S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{2}\end{array}\)

Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}}\)\( = \dfrac{1}{3}\dfrac{{a\sqrt 6 }}{2}\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 2 }}{4}\)

Chọn A.