Câu hỏi
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, \(AB = 6a,\,\,AC = 7a\) và \(AD = 4a\). Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD và DB. Thể tích V của tứ diện AMNP là:
- A \(V = \dfrac{7}{2}{a^3}\)
- B \(V = 14{a^3}\)
- C \(V = \dfrac{{28}}{3}{a^3}\)
- D \(V = 7{a^3}\)
Lời giải chi tiết:
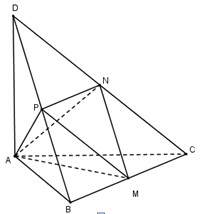
Dễ thấy BMNP là hình bình hành nên \(\widehat {PMN} = \widehat {PDN}\) (2 góc đối)
Tương tự ta có \(\widehat {NPM} = \widehat {NCM}\)
\( \Rightarrow \Delta BCD \sim \Delta NPM\left( {g.g} \right)\)
\( \Rightarrow \) Tỉ số đồng dạng \(k = \frac{{PN}}{{BC}} = \frac{1}{2}\)(do PN là đường trung bình của tam giác BCD)
\(\frac{{{S_{MNP}}}}{{{S_{BCD}}}} = {k^2} = \frac{1}{4} \Rightarrow {S_{MNP}} = \frac{1}{4}{S_{BCD}}\)
\( \Rightarrow \frac{{{V_{AMNP}}}}{{{V_{ABCD}}}} = \frac{{\frac{1}{3}d\left( {A;\left( {MNP} \right)} \right).{S_{MNP}}}}{{\frac{1}{3}d\left( {A;\left( {BCD} \right)} \right).{S_{BCD}}}} = \frac{1}{4} \Rightarrow {V_{AMNP}} = \frac{1}{4}{V_{ABCD}}\)
Mà \({V_{ABCD}} = \frac{1}{6}AB.AC.AD = \frac{1}{6}.6a.7a.4a = 28{a^3} \Rightarrow {V_{AMNP}} = \frac{1}{4}.28{a^3} = 7{a^3}\)
Chọn D.







