Câu hỏi
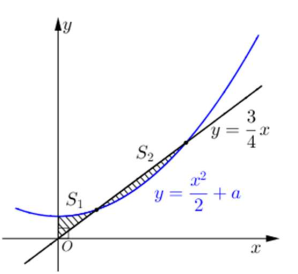
Cho đường thẳng \(y = \dfrac{3}{4}x\) và parabol \(y = \dfrac{1}{2}{x^2} + a\) (\(a\) là tham số thực dương). Gọi \({S_1}\) và \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình bên. Khi \({S_1} = {S_2}\) thì \(a\) thuộc khoảng nào dưới đây?
- A \(\left( {\dfrac{1}{4};\dfrac{9}{{32}}} \right)\).
- B \(\left( {\dfrac{3}{{16}};\dfrac{7}{{32}}} \right)\).
- C \(\left( {0;\dfrac{3}{{16}}} \right)\).
- D \(\left( {\dfrac{7}{{32}};\dfrac{1}{4}} \right)\).
Phương pháp giải:
- Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình có hai nghiệm phân biệt.
- Viết công thức tính hai phần diện tích \({S_1},{S_2}\).
- Sử dụng điều kiện \({S_1} = {S_2}\) tìm \(a\).
Lời giải chi tiết:
Phương trình hoành độ giao điểm : \(\dfrac{3}{4}x = \dfrac{1}{2}{x^2} + a \Leftrightarrow 2{x^2} - 3x + 4a = 0\,\,(*)\).
Ta có \((d)\) cắt \((P)\) tại 2 điểm phân biệt có hoành độ dương nên phương trình (*) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - 32a > 0\\2a > 0\end{array} \right. \Leftrightarrow 0 < a < \dfrac{9}{{32}}\).
Gọi hai nghiệm phân biệt của (*) là \({x_1} < {x_2}\).
Ta có : \({S_1} = \int\limits_0^{{x_1}} {\left( {\dfrac{1}{2}{x^2} - \dfrac{3}{4}x + a} \right){\rm{d}}x} = \left. {\left( {\dfrac{1}{6}{x^3} - \dfrac{3}{8}{x^2} + ax} \right)} \right|_0^{{x_1}} = \dfrac{1}{6}x_1^3 - \dfrac{3}{8}x_1^2 + a{x_1}\)
\({S_2} = \int\limits_{{x_1}}^{{x_2}} {\left( { - \dfrac{1}{2}{x^2} + \dfrac{3}{4}x - a} \right){\rm{d}}x} = \left. {\left( { - \dfrac{1}{6}{x^3} + \dfrac{3}{8}{x^2} - ax} \right)} \right|_{{x_1}}^{{x_2}}\)\( = \left( { - \dfrac{1}{6}x_2^3 + \dfrac{3}{8}x_2^2 - a{x_2}} \right) + \left( {\dfrac{1}{6}x_1^3 - \dfrac{3}{8}x_1^2 + a{x_1}} \right)\)
Do \({S_1} = {S_2}\) nên \(\dfrac{1}{6}x_1^3 - \dfrac{3}{8}x_1^2 + a{x_1} = = \left( { - \dfrac{1}{6}x_2^3 + \dfrac{3}{8}x_2^2 - a{x_2}} \right) + \left( {\dfrac{1}{6}x_1^3 - \dfrac{3}{8}x_1^2 + a{x_1}} \right)\)
\(\dfrac{1}{6}x_2^3 - \dfrac{3}{8}x_2^2 + a{x_2} = 0 \Leftrightarrow 4x_2^2 - 9{x_2} + 24a = 0\)
Do \({x_2}\) là nghiệm của phương trình (*) nên ta có hệ phương trình \(\begin{array}{l}\left\{ \begin{array}{l}2x_2^2 - 3{x_2} + 4a = 0\\4x_2^2 - 9{x_2} + 24a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x_2^2 - 3{x_2} + 4a = 0\\16a - 3{x_2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2.\dfrac{{256}}{9}{a^2} - 16a + 4a = 0\\{x_2} = \dfrac{{16a}}{3}\end{array} \right.\\ \Rightarrow \dfrac{{512}}{9}{a^2} - 12a = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\a = \dfrac{{27}}{{128}}\end{array} \right..\end{array}\)
Đối chiếu điều kiện của \(a\) nên ta có \(a = \dfrac{{27}}{{128}} \in \left( {\dfrac{3}{{16}};\dfrac{7}{{12}}} \right)\).
Chọn B.