Câu hỏi
Cho hàm số \(f\left( x \right)\), bảng biến thiên của hàm số \(f'\left( x \right)\) như sau:
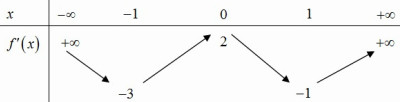
Số điểm cực trị của hàm số \(y = f\left( {4{x^2} - 4x} \right)\) là
- A \(9\)
- B \(5\)
- C \(7\)
- D \(3\)
Phương pháp giải:
- Tính \(y'\).
- Tìm số nghiệm bội lẻ của phương trình \(y' = 0\) và kết luận.
Lời giải chi tiết:
Ta có : \(y' = \left[ {f\left( {4{x^2} - 4x} \right)} \right]' = \left( {8x - 1} \right)f'\left( {4{x^2} - 4x} \right)\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\f'\left( {4{x^2} - 4x} \right) = 0\,\,\left( * \right)\end{array} \right.\)
Đặt \(t = 4{x^2} - 4x\) thì \(\left( * \right) \Leftrightarrow f'\left( t \right) = 0\).
Từ bảng biến thiên của hàm số \(f'\left( x \right)\) ta thấy, phương trình \(f'\left( t \right) = 0\) có bốn nghiệm \({t_1} < - 1 < {t_2} < 0 < {t_3} < 1 < {t_4}\)
Do đó \(f'\left( {4{x^2} - 4x} \right) = 0 \Leftrightarrow 4{x^2} - 4x = {t_i},i = \overline {1,4} \).
Xét \(t = 4{x^2} - 4x \Rightarrow t' = 8x - 4\) có bảng biến thiên :
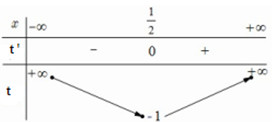
Từ bảng biến thiên ta thấy :
+) Phương trình \(4{x^2} - 4x = {t_1} < - 1\) vô nghiệm.
+) Phương trình \(4{x^2} - 4x = {t_2} \in \left( { - 1;0} \right)\) có hai nghiệm phân biệt.
+) Phương trình \(4{x^2} - 4x = {t_3} \in \left( {0;1} \right)\) có hai nghiệm phân biệt.
+) Phương trình \(4{x^2} - 4x = {t_4} > 1\) có hai nghiệm phân biệt.
Các nghiệm này đều không trùng nhau và khác \(\dfrac{1}{2}\).
Vậy có tất cả \(7\) điểm cực trị.
Chọn C.







