Câu hỏi
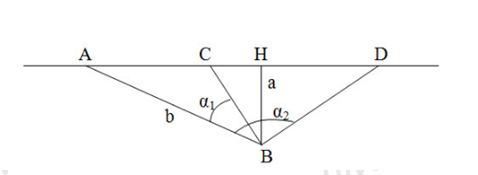
Xe bus chuyển động thẳng đều trên đường với \({v_1} = 16m/s\). Một hành khách đứng cách đường một đoạn \(a = 60m\), người này nhìn thấy xe bus vào thời điểm xe cách người một khoảng \(b = 400m\). Nếu muốn gặp xe với vận tốc nhỏ nhất thì người này phải chạy với vận tốc là bao nhiêu?
- A 1,2m/s
- B 3,6m/s
- C 2,4m/s
- D 3m/s
Phương pháp giải:
Phương pháp : Áp dụng điều kiện hai xe gặp nhau khi \({x_1}\; = {x_2}\;\)
Lời giải chi tiết:
Hướng dẫn giải:
Nếu muốn vận tốc là nhỏ nhất => quãng đường đi là nhỏ nhất => người đó đi theo hướng BH
Từ hình ta có: \(AH = \sqrt {{b^2} - {a^2}} = \sqrt {{{400}^2} - {{60}^2}} \approx 395.5(m)\)
Ta có: \(\frac{{BH}}{{{v_{\min }}}} = \frac{{AH}}{{{v_1}}} \to {v_{\min }} = \frac{{BH}}{{AH}}.{v_1} = \frac{{60}}{{395,5}}.16 = 2,4(m/s)\)
Chọn C
Câu hỏi trước
