Câu hỏi
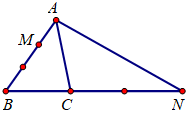
Cho \(\Delta ABC\) và các điểm \(M,\,\,N\) thỏa mãn \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} ,\,\,\,\overrightarrow {BN} = 3\overrightarrow {BC} .\) Đặt \(\overrightarrow a = \overrightarrow {AB} ,{\rm{ }}\overrightarrow b = \overrightarrow {AC} \). Chọn khẳng định đúng nhất.
- A \(\overrightarrow {CM} = \frac{1}{3}\overrightarrow a - \overrightarrow b \)
- B \(\overrightarrow {AN} = - 2\overrightarrow a + 3\overrightarrow b \)
- C \(\overrightarrow {MN} = - \frac{7}{3}\overrightarrow a + 3\overrightarrow b \)
- D Cả A, B, C đều đúng
Phương pháp giải:
Sử dụng quy tắc 3 điểm, quy tắc trừ để biến đổi.
Lời giải chi tiết:
Vì \(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} \Rightarrow \left\{ \begin{array}{l}M \in AB\\AM = \frac{1}{3}AB\end{array} \right..\)
Ta có: \(\overrightarrow {CM} = \overrightarrow {CA} + \overrightarrow {AM} = - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} = \frac{1}{3}\overrightarrow a - \overrightarrow b \)
\(\begin{array}{l}\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + 3\overrightarrow {BC} = \overrightarrow {AB} + 3\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = - 2\overrightarrow a + 3\overrightarrow b \\\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} = - \frac{1}{3}\overrightarrow a - 2\overrightarrow a + 3\overrightarrow b = - \frac{7}{3}\overrightarrow a + 3\overrightarrow b .\end{array}\)
Chọn C.