Phương pháp giải:

Chia cả tử và mẫu cho \({y^2}\), sử dụng phương pháp xét hàm số.

Lời giải chi tiết:

Theo bài ra ta có: \(P = \dfrac{{xy}}{{x + y + 1}} = \dfrac{{xy}}{{{x^2} + {y^2} + xy}}\).

TH1: \(y = 0 \Rightarrow P = 0\).

Khi đó \({x^2} = x + 1 \Leftrightarrow x = \dfrac{{1 \pm \sqrt 5 }}{2} \Rightarrow x + y \ne  - 1\,\,\left( {tm} \right)\).

TH2: \(y \ne 0\). Chia cả tử và mẫu của biểu thức \(P\) cho \({y^2}\) ta có:

\(P = \dfrac{{xy}}{{{x^2} + {y^2} + xy}} = \dfrac{{\dfrac{x}{y}}}{{{{\left( {\dfrac{x}{y}} \right)}^2} + 1 + \dfrac{x}{y}}}\)

Đặt \(t = \dfrac{x}{y}\), khi đó \(P = \dfrac{t}{{{t^2} + t + 1}} = f\left( t \right)\).

Ta có: \(f'\left( t \right) = \dfrac{{{t^2} + t + 1 - t\left( {2t + 1} \right)}}{{{{\left( {{t^2} + t + 1} \right)}^2}}} = \dfrac{{ - {t^2} + 1}}{{{{\left( {{t^2} + t + 1} \right)}^2}}} = 0 \Leftrightarrow t =  \pm 1\).

BBT:

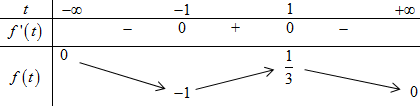
Từ BBT, kết hợp TH1 suy ra \(\left\{ \begin{array}{l}\min P =  - 1 = m\\\max P = \dfrac{1}{3} = M\end{array} \right. \Rightarrow M + m = \dfrac{{ - 2}}{3}\).

Chọn B