Phương pháp giải:

Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\,\,y = g\left( x \right),\,\,x = a,\,\,x = b\,\,\left( {a < b} \right)\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).

Lời giải chi tiết:

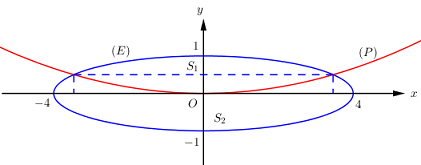
Parabol \(y = \dfrac{1}{{24}}{x^2}\) chia hình giới hạn bởi elip có phương trình \(\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{1} = 1 \Leftrightarrow y =  \pm \sqrt {1 - \dfrac{{{x^2}}}{{16}}} \) thành hai phần có diện tích lần lượt là \({S_1},\,\,{S_2}\,\,\left( {{S_1} < {S_2}} \right)\)được kí hiệu như hình vẽ.

Xét phương trình hoành độ giao điểm

\(\dfrac{1}{{24}}{x^2} = \sqrt {1 - \dfrac{{{x^2}}}{{16}}}  \Leftrightarrow \dfrac{{{x^4}}}{{576}} = 1 - \dfrac{{{x^2}}}{{16}} \Leftrightarrow {x^2} = 12 \Leftrightarrow x =  \pm 2\sqrt 3 \).

Khi đó ta có: \({S_1} = \int\limits_{ - 2\sqrt 3 }^{2\sqrt 3 } {\left( {\sqrt {1 - \dfrac{{{x^2}}}{{16}}}  - \dfrac{1}{{24}}{x^2}} \right)dx}  \approx 4,766\).

Diện tích elip là \({S_{\left( E \right)}} = \pi ab = \pi .4.1 = 4\pi  \Rightarrow {S_2} = {S_{\left( E \right)}} - {S_1} = 7,8\).

Vậy \(\dfrac{{{S_1}}}{{{S_2}}} \approx 0,6123\).

Chọn A