Phương pháp giải:

Cô lập \(m\).

Lời giải chi tiết:

ĐKXĐ: \(x \ge 0\).

TH1: \(x = 0 \Rightarrow 1 < 0\) (vô nghiệm).

TH2: \(x \ne 0 \Rightarrow x > 0\).

Ta có:

\(\begin{array}{l}\sqrt {\dfrac{m}{{72}}{x^2} + 1}  < \sqrt x  \Leftrightarrow 0 \le \dfrac{m}{{72}}{x^2} + 1 < x \Leftrightarrow m{x^2} - 72x + 72 < 0\\ \Leftrightarrow m{x^2} < 72x - 72 \Leftrightarrow m < \dfrac{{72}}{x} - \dfrac{{72}}{{{x^2}}} = f\left( x \right)\end{array}\)

Xét hàm số \(f\left( x \right) = \dfrac{{72}}{x} - \dfrac{{72}}{{{x^2}}}\) với \(x > 0\) ta có: \(f'\left( x \right) =  - \dfrac{{72}}{{{x^2}}} + \dfrac{{144}}{{{x^3}}} = 0 \Leftrightarrow \dfrac{{144 - 72x}}{{{x^3}}} = 0 \Leftrightarrow x = 2\).

BBT :

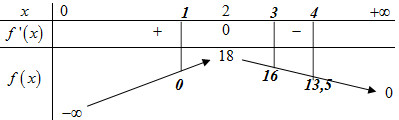
Để phương trình \(m < f\left( x \right)\) có tập nghiệm chứa đúng 2 nghiệm là số nguyên thì \(f\left( 4 \right) \le m < f\left( 3 \right) \Leftrightarrow \dfrac{{27}}{2} \le m < 16\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {14;15} \right\}\). Vậy tổng các giá trị của \(m\) là \(14 + 15 = 29\).

Chọn: B