Câu hỏi
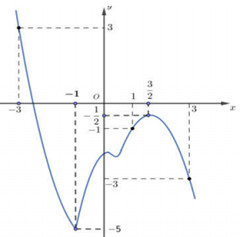
Cho hàm số \(f(x)\)liên tục trên R và có đồ thị như hình vẽ. Số giá trị nguyên của tham số \(m\)để phương trình: \(f\left( {3 - 4\sqrt {6x - 9{x^2}} } \right) + 1 + {m^2} = 0\) có nghiệm là:
- A 6
- B 4
- C 5
- D 7
Phương pháp giải:
+) Xác định tập giá trị của biểu thức \(3 - 4\sqrt {6x - 9{x^2}} \).
+) Dựa vào đồ thị hàm số, xác định giá trị của \( - \left( {1 + {m^2}} \right)\) để phương trình \(f\left( {3 - 4\sqrt {6x - 9{x^2}} } \right) + 1 + {m^2} = 0\) có nghiệm.
Lời giải chi tiết:
Ta có: \(0 \le \sqrt {6x - 9{x^2}} = \sqrt {1 - {{\left( {1 - 3x} \right)}^2}} \le 1 \Leftrightarrow - 1 \le 3 - 4\sqrt {6x - 9{x^2}} \le 3\).
Đặt \(t = 3 - 4\sqrt {6x - 9{x^2}} \Rightarrow t \in \left[ { - 1;3} \right]\). Yêu cầu bài toán trở thành tìm \(m\) để phương trình \(f\left( t \right) = - \left( {1 + {m^2}} \right)\) có nghiệm thuộc \(\left[ { - 1;3} \right]\) (1).
Quan sát đồ thị hàm số ta có:
\(\left( 1 \right) \Leftrightarrow - 5 \le - \left( {{m^2} + 1} \right) \le - \dfrac{1}{2} \Leftrightarrow \dfrac{1}{2} \le {m^2} + 1 \le 5 \Leftrightarrow - \dfrac{1}{2} \le {m^2} \le 4 \Leftrightarrow - 2 \le m \le 2\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1;2} \right\}\). Vậy có 5 giá trị của \(m\) thỏa mãn.
Chọn: C







