Phương pháp giải:

Áp dụng quy tắc cộng, nhân.

Lời giải chi tiết:

Số phần tử của không gian mẫu: \(n\left( \Omega  \right) = C_{10}^1.C_{10}^2.2 = 900\)

Tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy

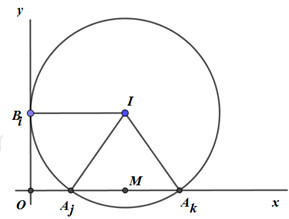
TH1: Đường tròn (I) tiếp xúc với Oy tại điểm \({B_i}\) và đi qua 2 điểm \({A_j},\,\,{A_k}\) (phân biệt):

Ta có: \(I{B_i} = I{A_j} = I{A_k} = r,\,\,O{B_i} = i,\,\,O{A_j} = j,\,\,O{A_k} = k,\,\,\left( {i,j,k \in \left\{ {1;2;...;10} \right\}} \right)\)

\(r = OM = \dfrac{{k + j}}{2} > i\)

\(\Delta I{A_j}M\) vuông tại M \( \Rightarrow IA_j^2 = MA_j^2 + I{M^2} \Leftrightarrow {\left( {\dfrac{{k + j}}{2}} \right)^2} = {\left( {\dfrac{{k - j}}{2}} \right)^2} + {i^2} \Leftrightarrow \dfrac{1}{2}kj = {i^2} \Leftrightarrow kj = 2{i^2}\)

Các bộ số \(\left( {i;j;k} \right)\) thỏa mãn là: \(\left( {3;1;9} \right),\,\,\left( {4;2;8} \right)\)

Số tam giác thỏa mãn là: \(2\).

TH2: Đường tròn (I) tiếp xúc với Ox tại điểm \({A_i}\) và đi qua 2 điểm \({B_j},\,\,{B_k}\) (phân biệt): ta được số tam giác thỏa mãn là 2.

Xác suất cần tìm là: \(P = \dfrac{{2 + 2}}{{900}} = \dfrac{1}{{225}}\)

Chọn: C