Câu hỏi
Cho hình chóp tứ giác đều \(S.ABC\) có tất cả các cạnh đều bằng \(1\). Gọi \(G\) là trọng tâm tam giác \(SBC\). Thể tích tứ diện \(SGCD\) bằng:
- A \(\dfrac{{\sqrt 2 }}{{36}}\)
- B \(\dfrac{{\sqrt 2 }}{6}\)
- C \(\dfrac{{\sqrt 3 }}{{36}}\)
- D \(\dfrac{{\sqrt 2 }}{{18}}\)
Phương pháp giải:
Tính tỉ lệ thể tích khối tứ diện \(SGCD\) và khối chóp \(S.ABCD\).
Lời giải chi tiết:
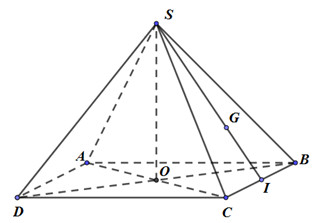
Gọi I là trung điểm của BC, do \(G\) là trọng tâm tam giác \(SBC \Rightarrow \dfrac{{SG}}{{SI}} = \dfrac{2}{3}\).
Ta có: \(\dfrac{{{V_{SGCD}}}}{{{V_{SICD}}}} = \dfrac{{SG}}{{SI}} = \dfrac{2}{3}\).
\({S_{\Delta DIC}} = \dfrac{1}{4}{S_{ABCD}} \Rightarrow {V_{S.CDI}} = \dfrac{1}{4}{V_{S.ABCD}} \Rightarrow {V_{SGCD}} = \dfrac{2}{3}.\dfrac{1}{4}{V_{S.ABCD}} = \dfrac{1}{6}{V_{S.ABCD}}\)
Ta có:
\(\begin{array}{l}OC = \dfrac{1}{2}AC = \dfrac{{\sqrt 2 }}{2},\,\,SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {1 - \dfrac{1}{2}} = \dfrac{{\sqrt 2 }}{2}\\ \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{\sqrt 2 }}{2}{.1^2} = \dfrac{{\sqrt 2 }}{6} \Rightarrow {V_{SGCD}} = \dfrac{1}{6}.\dfrac{{\sqrt 2 }}{6} = \dfrac{{\sqrt 2 }}{{36}}\end{array}\)
Chọn: A







