Câu hỏi
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
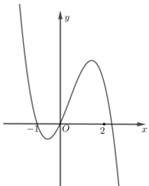
- A \(a + b + c + d < 0\)
- B \(a + c < b + d\)
- C \(a + c > 0\)
- D \(d + b - c > 0\)
Phương pháp giải:
Từ đồ thị hàm số suy ra \(f'\left( 0 \right) = 0;\,f'\left( x \right) > 0,\forall x \in \left( {0;1} \right)\)
Sử dụng ứng dụng tích phân tính diện tích hình phẳng: Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\) trục hoành, \(x = a,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
Lưu ý: \(\int\limits_a^b {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_a^b = f\left( b \right) - f\left( a \right)\)
Lời giải chi tiết:
Ta có \(f'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx + d\)
Từ đồ thị hàm số ta thấy \(f'\left( 0 \right) \Leftrightarrow d = 0\)
Lại có \(\int\limits_{ - 1}^0 {\left| {f'\left( x \right)} \right|dx} > 0 \Leftrightarrow \int\limits_0^{ - 1} {f'\left( x \right)dx} > 0 \Leftrightarrow \left. {f\left( x \right)} \right|_0^{ - 1} > 0 \Leftrightarrow f\left( { - 1} \right) > f\left( 0 \right)\)
\( \Leftrightarrow a - b + c - d + e > e \Leftrightarrow a + c > b + d\) nên B sai, lại có \(d = 0 \Rightarrow a + c > b\) (1)
+) Từ đồ thị suy ra \(f'\left( x \right) > 0;\,\forall x \in \left( {0;1} \right) \Rightarrow f\left( 1 \right) > f\left( 0 \right)\)
\( \Leftrightarrow a + b + c + d + e > e \Leftrightarrow a + b + c + d > 0\) nên A sai.
Mà \(d = 0\) nên \(a + b + c > 0 \Leftrightarrow a + c > - b\) (2)
Từ (1) và (2) suy ra \(2\left( {a + c} \right) > 0 \Leftrightarrow a + c > 0.\)
Chọn C.







