Câu hỏi
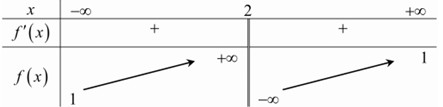
Bảng biến thiên sau đây là của hàm số nào?
- A \(f\left( x \right) = \dfrac{{x - 3}}{{x - 2}}\)
- B \(f\left( x \right) = \dfrac{{x + 3}}{{2 - x}}\)
- C \(f\left( x \right) = \dfrac{{x + 3}}{{x - 2}}\)
- D \(f\left( x \right) = \dfrac{{2x - 3}}{{x - 2}}\)
Phương pháp giải:
- Tìm các đường tiệm cận của đồ thị hàm số dựa vào bảng biến thiên.
- Nhận xét tính đơn điệu của hàm số.
- Đối chiếu với từng đáp án và kết luận.
Lời giải chi tiết:
Quan sát bảng biến thiên ta thấy:
- Đồ thị hàm số nhận đường thẳng \(x = 2\) làm TCĐ, đường thẳng \(y = 1\) là tiệm cận ngang nên loại B và D.
Lại có, hàm số đồng biến trên các khoảng xác định.
Xét đáp án A:
Có \(f'\left( x \right) = \dfrac{{ - 2 + 3}}{{{{\left( {x - 2} \right)}^2}}} = \dfrac{1}{{{{\left( {x - 2} \right)}^2}}} > 0,\forall x \ne 2\).
Do đó hàm số đồng biến trên các khoảng xác định, phù hợp với các yêu cầu ở trên.
Chọn A.







