Câu hỏi
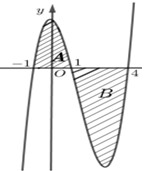
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Diện tích hai phần \(A\) và \(B\) lần lượt là \(\dfrac{{16}}{3}\) và \(\dfrac{{63}}{4}.\) Tính \(\int\limits_{ - 1}^{\frac{3}{2}} {f\left( {2x + 1} \right)dx} \).
- A \(\dfrac{{253}}{{12}}\)
- B \(\dfrac{{253}}{{24}}\)
- C \( - \dfrac{{125}}{{24}}\)
- D \( - \dfrac{{125}}{{12}}\)
Phương pháp giải:
Sử dụng phương pháp đổi biến số để đưa tích phân về biến \(t.\)
Sử dụng công thức \(\int\limits_a^c {f\left( x \right)d} x = \int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} \).
Lời giải chi tiết:
Xét \(\int\limits_{ - 1}^{\frac{3}{2}} {f\left( {2x + 1} \right)dx} \). Đặt \(2x + 1 = t \Leftrightarrow 2dx = dt \Leftrightarrow dx = \dfrac{{dt}}{2}\).
Đổi cận:\(\left\{ \begin{array}{l}x = - 1 \Rightarrow t = - 1\\x = \dfrac{3}{2} \Rightarrow t = 4\end{array} \right.\).
Khi đó ta có \(\int\limits_{ - 1}^{\dfrac{3}{2}} {f\left( {2x + 1} \right)dx} = \dfrac{1}{2}\int\limits_{ - 1}^4 {f\left( t \right)dt} = \dfrac{1}{2}\int\limits_{ - 1}^4 {f\left( x \right)dx} \)\( = \dfrac{1}{2}\left( {\int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} } \right)\)
Từ hình vẽ ta có \(\int\limits_{ - 1}^1 {f\left( x \right)dx} = \dfrac{{16}}{3};\,\int\limits_1^4 {f\left( x \right)dx} = - \dfrac{{63}}{4}\)
Nên \(\int\limits_{ - 1}^{\dfrac{3}{2}} {f\left( {2x + 1} \right)dx} = \dfrac{1}{2}\left( {\int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} } \right) = \dfrac{1}{2}\left( {\dfrac{{16}}{3} - \dfrac{{63}}{4}} \right) = - \dfrac{{125}}{{24}}\)
Chọn C.







