Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
Câu hỏi
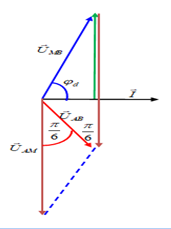
Cho mạch điện xoay chiều AB gồm hai đoạn mạch AM chỉ chứa C và đoạn mạch MB chỉ chứa cuộn dây mắc nối tiếp. Biết UAM =\(\sqrt{2}\)UMB và uAB nhanh pha \(\frac{\pi }{6}\)so với uAM. Biết hệ số công suất của cuộn dây không vượt quá giá trị 0,72. Hệ số công suất của cuộn dây bằng
- A \(\frac{\sqrt{5}+\sqrt{2}}{4}.\)
- B \(\frac{\sqrt{6}-\sqrt{2}}{4}.\)
- C \(\frac{\sqrt{5}-\sqrt{2}}{4
- D \(\frac{\sqrt{6}+\sqrt{2}}{4}.\)
Phương pháp giải:
Sử dụng giản đồ vec tơ
Áp dụng định lý hàm số sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
Lời giải chi tiết:
+ Dễ dàng nhận ra cuộn dây có điện trở thuần à \(0<\varphi <{{90}^{0}}\).
+ Áp dụng hàm sin trong tam giác, ta có: \(\frac{{{U}_{MB}}}{\sin \frac{\pi }{6}}=\frac{{{U}_{AM}}}{\sin ({{\varphi }_{d}}+\frac{\pi }{3})}\).
+ Chuẩn hóa: UMB =1 à \({{U}_{AM}}=\sqrt{2}.\)
=>\(\sin ({\varphi _d} + \frac{\pi }{3}) = \frac{1}{{\sqrt 2 }} \)
+\({\varphi _d} + \frac{\pi }{3} = \frac{\pi }{4} \to {\varphi _d} < 0:loai\)
+\({\varphi _d} + \frac{\pi }{3} = \frac{{3\pi }}{4} \to {\varphi _d} = \frac{{5\pi }}{{12}}\)
+ Hệ số công suất của cuộn dây: \(\text{cos}{{\varphi }_{d}}=c\text{os}\frac{5\pi }{12}=\)\(\frac{\sqrt{6}-\sqrt{2}}{4}\)
Chọn B