Câu hỏi
Cho số phức \(z\) có phần thực bằng \(\sqrt 2 \). Giá trị lớn nhất của \(\left| {\dfrac{1}{z} - i} \right|\) bằng
- A \(\sqrt 2 \).
- B \(1\).
- C \(1 + \sqrt 2 \).
- D \(2\)
Phương pháp giải:
Gọi \(z = \sqrt 2 + yi\,\,\left( {y \in \mathbb{R}} \right)\). Sử dụng phương pháp hàm số.
Lời giải chi tiết:
Gọi \(z = \sqrt 2 + yi\,\,\left( {y \in \mathbb{R}} \right)\). Theo bài ra ta có:
\(\left| {\dfrac{1}{z} - i} \right| = \dfrac{{\left| {1 - iz} \right|}}{{\left| z \right|}} = \dfrac{{\left| {1 - i\left( {\sqrt 2 + yi} \right)} \right|}}{{\sqrt {2 + {y^2}} }} = \sqrt {\dfrac{{2 + {{\left( {1 + y} \right)}^2}}}{{2 + {y^2}}}} = \sqrt {f\left( y \right)} \).
Xét hàm số
\(\begin{array}{l}f\left( y \right) = \dfrac{{2 + {{\left( {1 + y} \right)}^2}}}{{2 + {y^2}}} = \dfrac{{3 + 2y + {y^2}}}{{2 + {y^2}}} = 1 + \dfrac{{1 + 2y}}{{2 + {y^2}}}\\f'\left( y \right) = \dfrac{{2\left( {2 + {y^2}} \right) - \left( {1 + 2y} \right).2y}}{{{{\left( {2 + y} \right)}^2}}} = \dfrac{{4 + 2{y^2} - 2y - 4{y^2}}}{{{{\left( {2 + y} \right)}^2}}} = \dfrac{{ - 2{y^2} - 2y + 4}}{{{{\left( {2 + y} \right)}^2}}}\\f'\left( y \right) = 0 \Leftrightarrow - 2{y^2} - 2y + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}y = 1\\y = - 2\end{array} \right.\end{array}\)
BBT:
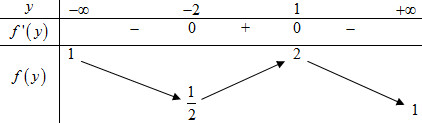
Từ BBT \( \Rightarrow \max f\left( y \right) = f\left( 1 \right) = 2 \Leftrightarrow \max \left| {\dfrac{1}{z} - i} \right| = \sqrt 2 \).
Chọn A.







