Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ
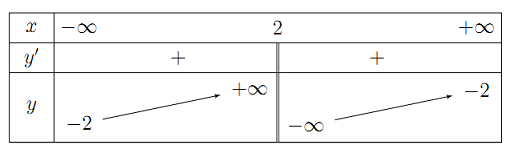
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
- A \(x = 2,y = - 2\).
- B \(x = - 2,y = 2\).
- C \(x = - 2,y = - 2\).
- D \(x = 2,y = 2\).
Phương pháp giải:
* Định nghĩa tiệm cận ngang của đồ thị hàm số \(y = f(x)\).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = a\,\)hoặc\(\,\mathop {\lim }\limits_{x \to - \infty } f(x) = a \Rightarrow y = a\) là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số \(y = f(x)\).
Nếu \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \,\)thì \(x = a\) là TCĐ của đồ thị hàm số.
Lời giải chi tiết:
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: \(x = 2,\,\,y = - 2\).
Chọn: A
Câu hỏi trước
