Câu hỏi
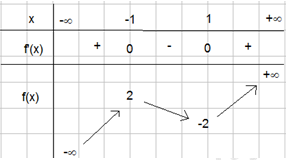
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f( - 2) = - 2,f(2) = 2\) và có bảng biến thiên như hình bên
Có bao nhiêu số tự nhiên m thỏa mãn phương trình \(f\left( { - f\left( x \right)} \right) \ge m\)có nghiệm thuộc đoạn \(\left[ { - 1;1} \right]\)?
- A \(1\)
- B \(2\)
- C \(3\)
- D \(4\)
Phương pháp giải:
+) Đặt \(t = f\left( x \right)\), xác định khoảng giá trị của \(t \in \left[ {a;b} \right]\).
+) Yêu cầu bài toán trở thành tìm \(m\) để bất phương trình \(f\left( t \right) \ge m\) có nghiệm thuộc đoạn \(\left[ {a;b} \right]\) \( \Rightarrow \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( t \right) \le m \le \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( t \right) = - 2 \le m \le 2\).
Lời giải chi tiết:
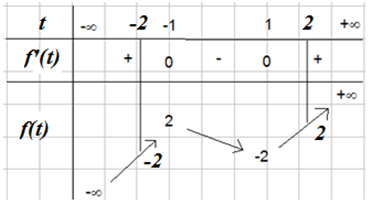
Với \(x \in \left[ { - 1;1} \right] \Rightarrow f\left( x \right) \in \left[ { - 2;2} \right] \Rightarrow - f\left( x \right) \in \left[ { - 2;2} \right]\).
Đặt \(t = f\left( x \right) \Rightarrow t \in \left[ { - 2;2} \right]\), yêu cầu bài toán trở thành tìm \(m\) để bất phương trình \(f\left( t \right) \ge m\) có nghiệm thuộc đoạn \(\left[ { - 2;2} \right]\) \( \Rightarrow \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( t \right) \le m \le \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( t \right) = - 2 \le m \le 2\).
Mà \(m \in \mathbb{N} \Rightarrow m \in \left\{ {0;1;2} \right\}\).
Chọn C.