Câu hỏi
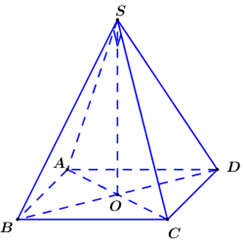
Cho hình chóp đều S.ABCD có ABCD là hình vuông cạnh 2a, tam giác SAC vuông. Bán kính mặt cầu ngoại tiếp tứ diện SABC bằng:
- A \(\frac{a}{{\sqrt 2 }}\)
- B \(a\)
- C \(a\sqrt 2 \)
- D \(2a\)
Phương pháp giải:
Xác định điểm cách đều 4 đỉnh của tứ diện sau đó tính bán kính.
Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow OA = OB = OC\,\,\left( 1 \right)\) (Do \(ABCD\) là hình vuông).
Tam giác \(SAC\) cân tại \(S\), lại là tam giác vuông \( \Rightarrow \Delta SAC\) vuông cân tại \(S\). Có \(SO\) là trung tuyến ứng với cạnh huyền \(AC \Rightarrow SO = \frac{1}{2}AC = OA = OC\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow OA = OB = OC = OS \Rightarrow O\) là tâm mặt cầu ngoại tiếp tứ diện \(S.ABC\).
\(ABCD\) là hình vuông cạnh \(2a \Rightarrow OA = \frac{{2a\sqrt 2 }}{2} = a\sqrt 2 = R\).
Chọn C.
Câu hỏi trước
