Câu hỏi
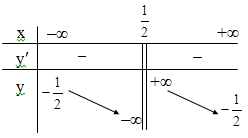
Cho hàm số \(y = f(x)\)có đạo hàm trên \(\mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\) và có bảng biến thiên như hình bên.Đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số đã cho lần lượt là
- A \(x = \frac{{ - 1}}{2},y = \frac{{ - 1}}{2}\)
- B \(x = \frac{1}{2},y = \frac{{ - 1}}{2}\)
- C \(x = \frac{{ - 1}}{2},y = \frac{1}{2}\)
- D \(x = \frac{1}{2},y = \frac{1}{2}\)
Phương pháp giải:
Dựa vào BBT để chọn đáp án đúng.
+) Đường thẳng \(x = a\) được gọi là TCĐ của đồ thị hàm số \(y = f\left( x \right) = \frac{{g\left( x \right)}}{{h\left( x \right)}} \Leftrightarrow \mathop {\lim }\limits_{x \to a} f\left( x \right) = \infty \) hoặc \(x = a\) là nghiệm của \(h\left( x \right) = 0\) mà không là nghiệm của \(g\left( x \right) = 0.\)
+) Đường thẳng \(y = b\) được gọi là TCN của đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow \mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = b.\)
Lời giải chi tiết:
Dựa vào BBT ta thấy: \(\mathop {\lim }\limits_{x \to \pm \infty } y = - \frac{1}{2} \Rightarrow y = - \frac{1}{2}\) là TCN của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} y = + \infty ;\,\,\,\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} y = - \infty \Rightarrow x = \frac{1}{2}\) là TCĐ của đồ thị hàm số.
Chọn B.