Câu hỏi
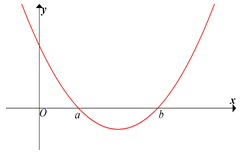
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) . Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Tìm tập hợp \(S\) tất cả các giá trị thực của tham số \(m\) để hàm số \(g\left( x \right) = \left| {2{f^2}\left( x \right) + 3f\left( x \right) + m} \right|\) có đúng 7 điểm cực trị, biết phương trình \(f'\left( x \right) = 0\) có đúng 2 nghiệm phân biệt, \(f\left( a \right) = 1\,,\,f\left( b \right) = 0\), \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \).
- A \(S = \left( { - 5;0} \right)\)
- B \(S = \left( { - 8;0} \right)\)
- C \(S = \left( { - 8;\frac{1}{6}} \right)\)
- D \(S = \left( { - 5;\frac{9}{8}} \right)\)
Phương pháp giải:
+ Sử dụng: Số cực trị của hàm số \(y = \left| {f\left( x \right) + m} \right|\) bằng tổng số điểm cực trị của hàm số \(y = f\left( x \right)\) và số nghiệm đơn (bội lẻ) của phương trình \(f\left( x \right) + m = 0\)
+ Từ đồ thị đã có ta lập BBT của hàm số \(y = f\left( x \right)\)
+ Số giao điểm của đường thẳng \(y = m\) và đồ thị hàm số \(y = f\left( x \right)\) là số nghiệm của phương trình \(f\left( x \right) = m.\)
+ Sử dụng công thức đạo hàm hàm hợp: \({\left( {f\left( u \right)} \right)^\prime } = u'.f'\left( u \right)\)
Lời giải chi tiết:
Xét hàm số \(h\left( x \right) = 2{f^2}\left( x \right) + 3f\left( x \right)\)
Ta có \(h'\left( x \right) = 4f\left( x \right).f'\left( x \right) + 3f'\left( x \right) = 0 \Leftrightarrow f'\left( x \right)\left( {4f\left( x \right) + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\f\left( x \right) = - \frac{3}{4}\end{array} \right.\)
+ Từ đồ thị hàm số \(y = f'\left( x \right)\) ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\\x = b\end{array} \right.\)
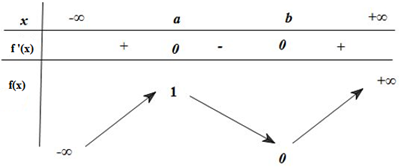
+ Từ đồ thị hàm số \(y = f'\left( x \right)\) ta có BBT của hàm số \(y = f\left( x \right)\)
Với \(x = a \Rightarrow f\left( a \right) = 1;\,x = b \Rightarrow f\left( b \right) = 0\)
Từ đó \(f\left( x \right) = \frac{{ - 3}}{4}\) có 1 nghiệm \(x = {x_0} < a.\)
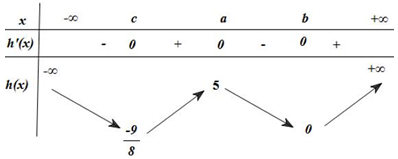
Khi đó \(h'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_0} < a \Rightarrow h\left( {{x_0}} \right) = 2f{\left( {{x_0}} \right)^2} + 3f\left( {{x_0}} \right) = 2.{\left( { - \frac{3}{4}} \right)^2} - 3.\frac{3}{4} = - \frac{9}{8}\\x = a \Rightarrow h\left( a \right) = 2{f^2}\left( a \right) + 3f\left( a \right) = 5\\x = b \Rightarrow h\left( b \right) = 2{f^2}\left( b \right) + 3f\left( b \right) = 0\end{array} \right.\)
Ta có BBT của hàm số \(h\left( x \right)\)
Từ đó hàm số \(h\left( x \right)\) có ba điểm cực trị.
Ta nhận thấy số điểm cực trị của hàm số \(y = h\left( x \right)\) bằng với số điểm cực trị của hàm số \(y = h\left( x \right) + m\)
Và số điểm cực trị của hàm số \(y = \left| {h\left( x \right) + m} \right|\) bằng tổng số điểm cực trị của hàm số \(y = h\left( x \right) + m\) và số nghiệm đơn ( nghiệm bội lẻ) của phương trình \(h\left( x \right) + m = 0 \Leftrightarrow h\left( x \right) = - m\)
Từ đó suy ra để hàm số \(y = \left| {h\left( x \right) + m} \right|\) có 7 điểm cực trị thì phương trình \(h\left( x \right) = - m\) có 4 nghiệm phân biệt.
Từ BBT suy ra \(0 < - m < 5 \Leftrightarrow - 5 < m < 0\).
Suy ra \(S = \left( { - 5;0} \right)\).
Chọn A.