Câu hỏi
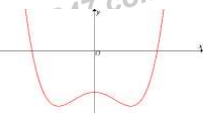
Cho hàm số \(y = a{x^4} + b{x^2} + c\,\,\,\left( {a \ne 0} \right)\) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?.
- A \(a > 0,b > 0,c < 0\).
- B \(a < 0,b > 0,c < 0\).
- C \(a > 0,b < 0,c < 0\).
- D \(a > 0,b > 0,c > 0\).
Phương pháp giải:
Nhận xét dáng đồ thị hàm số, điểm đi qua, số điểm cực trị và suy ra dấu của \(a,b,c\).
Lời giải chi tiết:
Quan sát đồ thị hàm số ta thấy \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \) nên \(a > 0\).
Đồ thị hàm số đi qua điểm \(\left( {0;c} \right)\) nằm dưới trục hoành nên \(c < 0\).
Dồ thị hàm số có ba điểm cực trị nên \(y' = 0\) có ba nghiệm phân biệt
\( \Leftrightarrow 4a{x^3} + 2bx = 0\) có ba nghiệm phân biệt \( \Leftrightarrow 2a{x^2} + b = 0\) có hai nghiệm phân biệt khác \(0\)
\( \Leftrightarrow - \frac{b}{{2a}} > 0 \Leftrightarrow b < 0\) (do \(a > 0\)).
Vậy \(a > 0,b < 0,c < 0\).
Chọn C.