Câu hỏi
Cho tứ diện S.ABC có SA, SB, SC đôi một vuông góc và \(SA = SB = SC\) . Gọi I, J lần lượt là trung điểm của AB, BC. Tính góc giữa hai mặt phẳng (SAJ) và (SCI)?
- A \({30^0}\)
- B \({60^0}\)
- C \({90^0}\)
- D \({120^0}\)
Phương pháp giải:
+) Chứng minh chóp S.ABC là chóp đều.
+) Gọi H là tâm tam giác đều ABC \( \Rightarrow SH \bot \left( {ABC} \right)\)
+) Chứng minh AJ và CI cùng vuông góc với giao tuyến SH.
+) Sử dụng tính chất hai góc nhọn trong tam giác vuông phụ nhau.
Lời giải chi tiết:
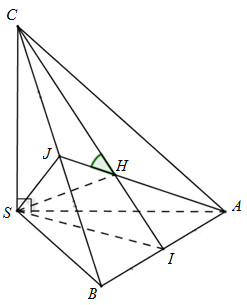
Vì \(SA = SB = SC\) nên \(AB = BC = CA\). Suy ra chóp S.ABC đều.
Gọi H là tâm tam giác đều ABC\( \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot CI;SH \bot AJ\)
Ta có: \(\left. \begin{array}{l}\left( {SAJ} \right) \cap \left( {SCI} \right) = SH\\AJ \bot SH\\CI \bot SH\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAJ} \right);\left( {SCI} \right)} \right)} = \widehat {\left( {AJ;CI} \right)} = \widehat {CHJ}\)
(Vì tam giác CHJ vuông tại J nên \(\widehat {CHJ} < {90^0}\))
Vì tam giác ABC đều nên trung tuyến CI đồng thời là phân giác\( \Rightarrow \widehat {JCH} = {30^0}\)
Xét tam giác vuông CHJ có: \(\widehat {CHJ} = {90^0} - \widehat {JCH} = {90^0} - {30^0} = {60^0}\)
Chọn B.







