Phương pháp giải:

+) Xác định góc giữa mặt phẳng (SBC) và mặt đáy bằng cách xác định hai đường thẳng lần lượt thuộc hai mặt và cùng vuông góc với giao tuyến BC.

+) Gọi D là trung điểm của SA.

+) Chứng minh \(BD \bot SA\) bằng cách chứng minh tam giác SAB đều.

+) Chứng minh \(CD \bot SA\) bằng cách chứng minh tam giác SCA cân tại C.

+) Chứng minh \( \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SAC} \right)} \right)} = \widehat {\left( {CD;BD} \right)}\)

+) Áp dụng định lí Cosin trong tam giác.

Lời giải chi tiết:

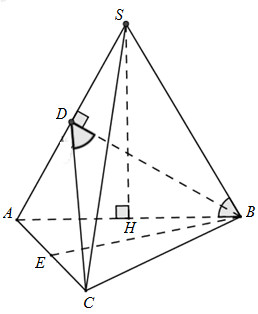
Ta có: \(\left. \begin{array}{l}BC \bot AB\\BC \bot SH\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)

\(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SB \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}\)

Lại có: H là trung điểm của AB mà \(SH \bot AB\) nên tam giác SAB cân tại S

có góc SBA = 60⁰ nên

\( \Rightarrow \Delta SAB\) đều. Gọi D là trung điểm của SA \( \Rightarrow BD \bot SA\)

\(\left( {SAC} \right) \cap \left( {SAB} \right) = SA\)

Ta có: 

\(\begin{array}{l}BD = \frac{{4\sqrt 3 }}{2} = 2\sqrt 3 ;SD = AD = \frac{1}{2}SA = \frac{1}{2}AB = 2;\\AC = 4\sqrt 2 ;SC = \sqrt {S{B^2} + B{C^2}}  = \sqrt {{4^2} + {4^2}}  = 4\sqrt 2 \end{array}\)

\( \Rightarrow \Delta SAC\) cân tại C \( \Rightarrow CD \bot SA\)

\(\left. \begin{array}{l}\left( {SAC} \right) \cap \left( {SAB} \right) = SA\\CD \bot SA\\BD \bot SA\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SAC} \right)} \right)} = \widehat {\left( {CD;BD} \right)}\)

Ta có:\(CD = \sqrt {A{C^2} - A{D^2}}  = \sqrt {32 - 4}  = 2\sqrt 7 \)\( \Rightarrow cos\widehat {BDC} = \dfrac{{B{D^2} + C{D^2} - B{C^2}}}{{2.BD.CD}} = \dfrac{{12 + 28 - 16}}{{2.2\sqrt 3 .2\sqrt 7 }} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }}\)

Chọn C.