Câu hỏi
Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\). Biết rằng hàm số \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Hỏi hàm số \(y = f\left( {2x - {x^2}} \right)\) có bao nhiêu điểm cực đại?
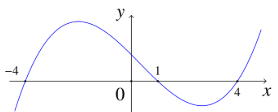
- A \(5\)
- B \(3\)
- C \(1\)
- D \(2\)
Phương pháp giải:
+) Tính đạo hàm của hàm số \(y = f\left( {2x - {x^2}} \right)\).
+) Xét dấu, lập BBT (hoặc BXD) và kết luận số điểm cực đại của hàm số.
Lời giải chi tiết:
\(\begin{array}{l}y = f\left( {2x - {x^2}} \right) = g\left( x \right) \Rightarrow g'\left( x \right) = \left( {2 - 2x} \right)f'\left( {2x - {x^2}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2 - 2x = 0\\f'\left( {2x - {x^2}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\2x - {x^2} = - 4\\2x - {x^2} = 1\\2x - {x^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1 \pm \sqrt 5 \\x = 1\,\,\left( {boi\,\,2} \right)\end{array} \right.\end{array}\)
BBT:

Dựa vào BBT ta thấy hàm số \(y = f\left( {2x - {x^2}} \right)\) có 1 điểm cực đại.
Chọn C







