Câu hỏi
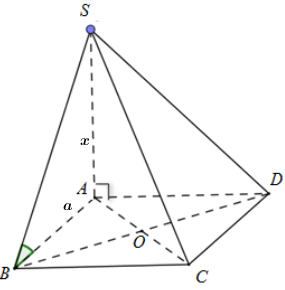
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA vuông góc với đáy, SA = x. Xác định x để hai mặt phẳng (SBC) và (ABC) tạo với nhau một góc \({60^0}\) ?
- A \(x = a\)
- B \(x = a\sqrt 2 \)
- C \(x = 2a\)
- D \(x = a\sqrt 3 \)
Phương pháp giải:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến của hai mặt phẳng đó.
Sử dụng các hàm lượng giác để tìm x theo a.
Lời giải chi tiết:
Ta có: \(\left. \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right\} \Rightarrow BC \bot SB\)
\(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SB \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}\)
Vì \(\widehat {SBA} < {90^0}\) nên ta có: \(\tan \widehat {SBA} = \frac{{SA}}{{AB}} \Rightarrow \sqrt 3 = \frac{x}{a} \Rightarrow x = a\sqrt 3 \) .
Chọn D.