Câu hỏi
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a tâm O, \(SO \bot \left( {ABCD} \right)\). Tính góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\)?
- A \({60^0}\)
- B \({90^0}\)
- C \({120^0}\)
- D \({150^0}\)
Phương pháp giải:
Hai mặt phẳng vuông góc thì góc giữa chúng bằng 900.
Lời giải chi tiết:
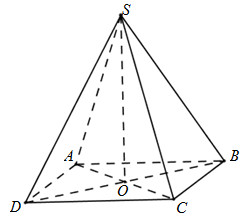
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}BD \bot SO\\BD \bot AC\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right)\\ \Rightarrow \widehat {\left( {\left( {SAC} \right);\left( {SBD} \right)} \right)} = {90^0}\end{array}\)
Chọn B.
Câu hỏi trước
