Môn Lý - Lớp 12
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng cao
Câu hỏi
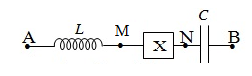
Đoạn mạch nối tiếp gồm cuộn cảm thuần, đoạn mạch X và tụ điện (hình vẽ).
Khi đặt vào hai đầu A, B điện áp \({{u}_{AB}}\text{ }=\text{ }{{U}_{O}}cos\left( \omega t\text{ }+\text{ }\varphi \right)\) (V);
\(Uo,\omega \) và không đổi thì: \(LC{{\omega }^{2}}=1\), ${{U}_{AN}}=30\sqrt{2}V$ và ${{U}_{MB}}=60\sqrt{2}V$, đồng thời UMB trễ pha so với UAN . Nếu cảm kháng của cuộn dây là 15W thì công suất của đoạn mạch A, B có giá trị gần đúng nhất là
- A 79 W
- B 104 W
- C 60 W
- D 112W
Phương pháp giải:
Sử dụng giản đồ vecto
Sử dụng các định lí hàm số sin, hàm số cos:
\(\begin{array}{l}
{c^2} = {a^2} + {b^2} - 2ab.cos\varphi \\
\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}
\end{array}\)
Công suất của mạch: \(P=UI\cos \varphi \)
Lời giải chi tiết:
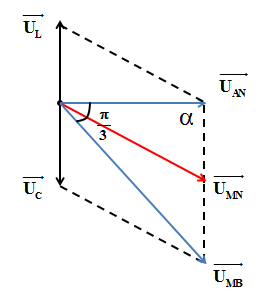
Áp dụng định lý hàm số cos:
\(\frac{{{U_L} + {U_C}}}{{\sin \frac{\pi }{3}}} = \frac{{{U_{MB}}}}{{\sin \alpha }} \Rightarrow \sin \alpha = \frac{{60\sqrt 2 .\sin \frac{\pi }{3}}}{{30\sqrt 6 }} = 1 \Rightarrow \alpha = {90^o}\)
Lại có \(LC{{\omega }^{2}}=1\)
\(\Rightarrow {{U}_{L}}={{U}_{C}}=15\sqrt{6}(V)\)
Dòng điện trong mạch: \(I=\frac{{{U}_{L}}}{{{Z}_{L}}}=\frac{15\sqrt{6}}{15}=\sqrt{6}\) (A)
Áp dụng định lý hàm số sin:\(\frac{{{U}_{L}}+{{U}_{C}}}{\sin \frac{\pi }{3}}=\frac{{{U}_{MB}}}{\sin \alpha }\Rightarrow \sin \alpha =\frac{60\sqrt{2}.\sin \frac{\pi }{3}}{30\sqrt{6}}=1\Rightarrow \alpha ={{90}^{o}}\) :
\(\Rightarrow {{U}_{MN}}=\sqrt{U_{AN}^{2}+U_{L}^{2}}=15\sqrt{14}\) (V)
Vì \({{U}_{L}}={{U}_{C}}\to {{U}_{AB}}={{U}_{MN}}\), \(\text{cos}\varphi \text{=}\frac{{{U}_{AN}}}{{{U}_{MN}}}=\frac{2\sqrt{7}}{7}\)
Công suất của mạch: \(P=UI\cos \varphi =60\sqrt{3}\approx 104\) (W)
Chọn B
Câu hỏi trước
