Phương pháp giải:

Phân chia khối hộp ra các phần, lập tỉ số thể tích.

Lời giải chi tiết:

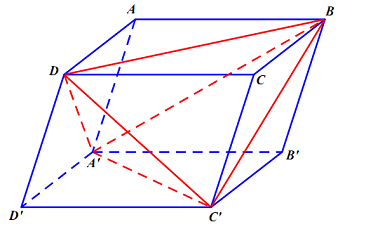
Gọi V là thể tích khối hộp ABCD.A’B’C’D’.

Ta có: \({V_{A.A'BD}} = {V_{B'.A'BC'}} = {V_{C.BDC'}} = {V_{D'.A'C'D'}} = \dfrac{1}{6}V\)

Mà \(V = {V_{ABC.A'B'C'D'}} = {V_{BDA'C'}} + {V_{AA'BD}} + {V_{B'A'BC'}} + {V_{CBDC'}} + {V_{D'A'C'D}} = {V_{BDA'C'}} + \dfrac{4}{6}V\)

\( \Rightarrow {V_{BDA'C'}} = \dfrac{1}{3}V \Rightarrow \dfrac{{{V_{BDA'C'}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{3}\).

Chọn: C