Câu hỏi
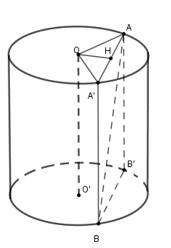
Cho hình trụ có tâm hai đáy lần lượt là \(O\) và \(\left( {O'} \right)\) ; bán kính đáy hình trụ bằng \(a.\) Trên hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) lần lượt lấy hai điểm \(A\) và \(B\) sao cho đường thẳng \(AB\) tạo với trục của hình trụ một góc \(30^\circ \) và có khoảng cách tới trục của hình trụ bằng \(\dfrac{{a\sqrt 3 }}{2}\) . Tính diện tích toàn phần của hình trụ đã cho.
- A \(\dfrac{{\pi {a^2}}}{3}\left( {\sqrt 3 + 2} \right)\)
- B \(\pi {a^2}\left( {\sqrt 3 + 2} \right)\)
- C \(2\pi {a^2}\left( {\sqrt 3 + 1} \right)\)
- D \(\dfrac{{2\pi {a^2}}}{3}\left( {\sqrt 3 + 3} \right)\)
Phương pháp giải:
+ Sử dụng \(d\left( {a;b} \right) = d\left( {a;\left( P \right)} \right) = d\left( {M;\left( P \right)} \right) = MH\) với \(a//\left( P \right);\,\,\,b \subset \left( P \right);\,\,\,M \in a\) và \(H\) là hình chiếu vuông góc của \(M\) xuống mặt phẳng \(\left( P \right).\)
+ Xác định góc giữa hai đường thẳng \(a,b\) là góc giữa \(a\) và \(b'\) với \(b//b'.\)
+ Sử dụng định lý Pytago và tỉ số lượng giác của góc nhọn.
+ Diện tích toàn phần của hình trụ có bán kính đáy \(r\) và đường sinh \(l\) là \({S_{tp}} = 2\pi rl + 2\pi {r^2}\)
Lời giải chi tiết:
Kẻ các đường sinh \(AB',A'B\) thì \(AB'//OO'//A'B\)
Ta có \(d\left( {OO';AB} \right) = d\left( {OO';\left( {AA'BB'} \right)} \right) = d\left( {O;\left( {AA'BB'} \right)} \right)\)
Kẻ \(OH \bot AA'\) tại \(H \Rightarrow H\) là trung điểm của \(AA'.\)
Ta có \(\left\{ \begin{array}{l}OH \bot AA'\\\,A'B \bot OH\end{array} \right. \Rightarrow OH \bot \left( {AA'BB'} \right) \Rightarrow d\left( {O;\left( {AA'BB'} \right)} \right) = OH = \dfrac{{a\sqrt 3 }}{2}\)
Lại có \(AB\) tạo với trục hình trụ góc \({30^0}\) mà \(OO'//A'B \Rightarrow \widehat {A'BA} = 30^\circ \)
Xét tam giác \(OHA\) vuông tại \(H\) có:
\(HA = \sqrt {O{A^2} - O{H^2}} = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}} = \dfrac{a}{2}\) suy ra \(AA' = 2HA = a\)
Xét tam giác \(ABA'\) vuông tại \(A'\) có \(A'B = AA'.\cot 30^\circ = a\sqrt 3 \)
Diện tích toàn phần của hình trụ đã cho là:
\({S_{tp}} = 2\pi rl + 2\pi {r^2} = 2\pi .a.a\sqrt 3 + 2\pi {a^2} = 2\pi {a^2}\left( {\sqrt 3 + 1} \right)\)
Chọn C.