Câu hỏi
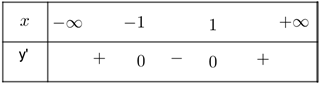
Cho hàm số \(y = f(x)\) là một hàm đa thức có bảng xét dấu của \(f'(x)\) như sau:
Số điểm cực trị của hàm số \(g(x) = f\left( {{x^2} - \left| x \right|} \right)\) là:
- A \(5\)
- B \(3\)
- C \(7\)
- D \(1\)
Lời giải chi tiết:
Ta có
\(\begin{array}{l}g\left( x \right) = f\left( {{x^2} - \left| x \right|} \right) = \left[ \begin{array}{l}f\left( {{x^2} - x} \right)\,\,khi\,\,x \ge 0\\f\left( {{x^2} + x} \right)\,\,khi\,\,x < 0\end{array} \right.\\ \Rightarrow g'\left( x \right) = \left[ \begin{array}{l}\left( {2x - 1} \right)f'\left( {{x^2} - x} \right)\,\,khi\,\,x \ge 0\\\left( {2x + 1} \right)f'\left( {{x^2} + x} \right)\,\,khi\,\,x < 0\end{array} \right.\\ \Rightarrow g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 0\,\,khi\,\,x \ge 0\\f'\left( {{x^2} - x} \right) = 0\,\,khi\,\,x \ge 0\\2x + 1 = 0\,\,khi\,\,x < 0\\f'\left( {{x^2} + x} \right) = 0\,\,khi\,\,x < 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{2}\,\,\left( {tm} \right)\\{x^2} - x = - 1\,\,khi\,\,x \ge 0\\{x^2} - x = 1\,\,khi\,\,x \ge 0\\x = - \frac{1}{2}\,\,\left( {tm} \right)\\{x^2} + x = - 1\,\,khi\,\,x < 0\\{x^2} + x = 1\,\,khi\,\,x < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm \frac{1}{2}\\x = \frac{{1 + \sqrt 5 }}{2}\\x = \frac{{ - 1 - \sqrt 5 }}{2}\end{array} \right.\end{array}\)
Qua 4 điểm trên, \(g'\left( x \right)\) đều đổi dấu.
Lại có \(g'\left( x \right)\) đổi dấu khi qua điểm \(x = 0\).
Do đó hàm số có tất cả 5 điểm cực trị.
Chọn A.