Câu hỏi
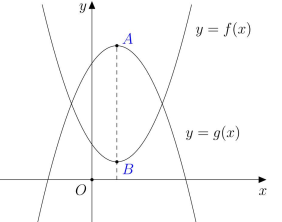
Cho hai hàm đa thức \(y = f\left( x \right),y = g\left( x \right)\) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thịhàm số \(y = f\left( x \right)\) có đúng một điểm cực trị là \(A,\) đồ thị hàm số \(y = g\left( x \right)\) có đúng một điểm cực trịlà \(B\) và \(AB = \dfrac{7}{4}.\) Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( { - 5;5} \right)\) để hàm số\(y = \left| {\left| {f\left( x \right) - g\left( x \right)} \right| + m} \right|\)có đúng 5 điểm cực trị?
- A \(1\)
- B \(3\)
- C \(4\)
- D \(6\)
Phương pháp giải:
Lập BBT của hàm số \(k\left( x \right) = \left| {f\left( x \right) - g\left( x \right)} \right|\) từ đó tìm số cực trị của hàm số \(y = k\left( x \right) + m\)
Sử dụng nhận xét: Số điểm cực trị của đồ thị hàm số \(y = \left| {f\left( x \right) + m} \right|\) bằng tổng số điểm cực trị của hàm số \(f\left( x \right) + m\) và số nghiệm đơn (hay bội lẻ) của phương trình \(f\left( x \right) + m = 0.\)
Lời giải chi tiết:
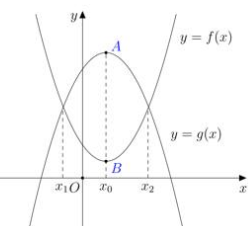
Ta có hàm số \(f\left( x \right)\) có 1 điểm cực trị \(x = {x_0}\) và \(g\left( x \right)\) có 1 điểm cực trị \(x = {x_0}\) nên suy ra \(f'\left( {{x_0}} \right) = 0;\,g'\left( {{x_0}} \right) = 0\)
Xét hàm số \(h\left( x \right) = f\left( x \right) - g\left( x \right) \Rightarrow h'\left( x \right) = f'\left( x \right) - g'\left( x \right)\), khi đó \(h'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) - g'\left( x \right) = 0 \Rightarrow x = {x_0}\)
Lại có \(h\left( {{x_0}} \right) = f\left( {{x_0}} \right) - g\left( {{x_0}} \right) = - \dfrac{7}{4}\) (theo giả thiết)
Từ đồ thị hàm số ta thấy \(f\left( {{x_1}} \right) = g\left( {{x_1}} \right);\,f\left( {{x_2}} \right) = g\left( {{x_2}} \right)\) nên \(h\left( x \right) = 0 \Leftrightarrow f\left( x \right) - g\left( x \right) = 0 \Leftrightarrow f\left( x \right) = g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = {x_2}\end{array} \right.\)
Bảng biến thiên của hàm số \(h\left( x \right)\) là
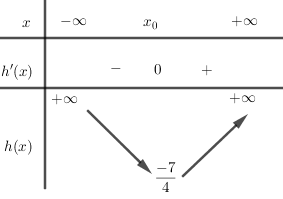
Từ đó ta có BBT của hàm số \(k\left( x \right) = \left| {f\left( x \right) - g\left( x \right)} \right|\)
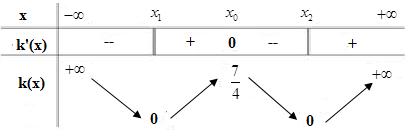
Từ BBT ta thấy hàm số \(y = k\left( x \right)\) có ba điểm cực trị nên hàm số \(y = k\left( x \right) + m\) cũng có 3 điểm cực trị.
Nhận thấy số điểm cực trị của hàm số \(y = \left| {k\left( x \right) + m} \right|\) bằng tổng số điểm cực trị của hàm số \(y = k\left( x \right) + m\) và số nghiệm đơn (hay nghiệm bội lẻ) của phương trình \(k\left( x \right) + m = 0\).
Suy ra để hàm số \(y = \left| {k\left( x \right) + m} \right|\) có đúng 5 điểm cực trị thì phương trình \(k\left( x \right) + m = 0 \Leftrightarrow k\left( x \right) = - m\) có hai nghiệm đơn (hay bội lẻ). Từ BBT ta có \( - m > \dfrac{7}{4}\)\( \Leftrightarrow m < - \dfrac{7}{4}\) mà \(m \in \mathbb{Z},m \in \left( { - 5;5} \right) \Rightarrow m \in \left\{ { - 4; - 3; - 2} \right\}\)
Vậy có 3 giá trị của \(m\) thỏa mãn.
Chọn B







