Phương pháp giải:

- Dựng hình chiếu của \(O\) lên \(\left( {O'MN} \right)\) và tâm đáy hình nón.

- Diện tích xung quanh hình nón \(S = \pi Rl\) với \(R\) là bán kính đáy, \(l\) là độ dài đường sinh

Lời giải chi tiết:

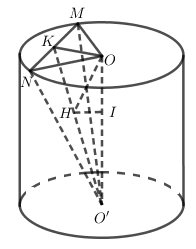
Gọi \(K\) là trung điểm của \(MN\), \(H\) là hình chiếu của \(O\) lên \(O'K\), \(I\) là hình chiếu của \(H\) lên \(O'O\).

Dễ thấy \(MN \bot \left( {OKO'} \right) \Rightarrow MN \bot OH\). Do đó \(OH \bot \left( {O'MN} \right)\).

Ta có : \(\Delta OMN\) đều cạnh \(r\) nên \(OK = \dfrac{{r\sqrt 3 }}{2}\), mà \(OO' = \dfrac{{3r}}{2}\)

\( \Rightarrow OH = \dfrac{{OK.OO'}}{{\sqrt {O{K^2} + O'{O^2}} }} = \dfrac{{\dfrac{{r\sqrt 3 }}{2}.\dfrac{{3r}}{2}}}{{\sqrt {\dfrac{{3{r^2}}}{4} + \dfrac{{9{r^2}}}{4}} }} = \dfrac{{3r}}{4}\).

Lại có \(O'K = \sqrt {O'{O^2} + O{K^2}}  = r\sqrt 3 ,\,\,\,O'H = \dfrac{{O'{O^2}}}{{O'K}} = \dfrac{{3r\sqrt 3 }}{4}\)

\( \Rightarrow \dfrac{{HI}}{{OK}} = \dfrac{{O'H}}{{O'K}} = \dfrac{{\dfrac{{3r\sqrt 3 }}{4}}}{{r\sqrt 3 }} = \dfrac{3}{4} \Rightarrow HI = \dfrac{3}{4}OK = \dfrac{3}{4}.\dfrac{{r\sqrt 3 }}{2} = \dfrac{{3r\sqrt 3 }}{8}\)

Diện tích xung quanh \({S_{xq}} = \pi .HI.OH = \pi .\dfrac{{3r\sqrt 3 }}{8}.\dfrac{{3r}}{4} = \dfrac{{9\sqrt 3 \pi {r^2}}}{{32}}\).

Chọn A