Câu hỏi
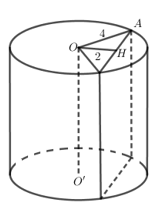
Cho hình trụ có trục \(OO'\) và có bán kính đáy bằng \(4\). Một mặt phẳng song song với trục \(OO'\) và cách \(OO'\) một khoảng bằng \(2\) cắt hình trụ theo thiết diện là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng
- A \(26\sqrt 3 \pi \)
- B \(8\sqrt 3 \pi \)
- C \(16\sqrt 3 \pi \)
- D \(32\sqrt 3 \pi \)
Phương pháp giải:
Tính chiều cao hình trụ và tính diện tích xung quanh theo công thức \({S_{xq}} = 2\pi Rh\).
Lời giải chi tiết:
Ta có : \(\Delta OHA\) vuông tại \(H\) có \(OH = 2,OA = 4 \Rightarrow AH = \sqrt {O{A^2} - O{H^2}} = 2\sqrt 3 \).
Thiết diện là hình vuông có cạnh \(2AH = 2.2\sqrt 3 = 4\sqrt 3 \) \( \Rightarrow h = OO' = 4\sqrt 3 \).
Diện tích xung quanh \(S = 2\pi Rh = 2\pi .4.4\sqrt 3 = 32\pi \sqrt 3 \).
Chọn D.
Câu hỏi trước
