Phương pháp giải:

hể tích khối nón có bán kính đáy \(r\) và đường cao \(h\) là \(V = \dfrac{1}{3}\pi {r^2}h\)

Lời giải chi tiết:

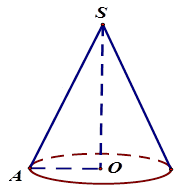
Hình nón đỉnh \(S\) có bán kính đáy \(OA = a;\) góc giữa đường  sinh và đáy là \(\widehat {SAO} = {30^0}\).

Xét tam giác \(SAO\) vuông tại \(O\) có \(SO = OA.\tan \widehat {SAO} = a.\tan {30^0} = \dfrac{{a\sqrt 3 }}{3}\)

Thể tích khối nón \(V = \dfrac{1}{3}\pi A{O^2}.SO = \dfrac{1}{3}\pi {a^2}.\dfrac{{a\sqrt 3 }}{3} = \dfrac{{\pi {a^3}\sqrt 3 }}{9}\).

Chọn D