Câu hỏi
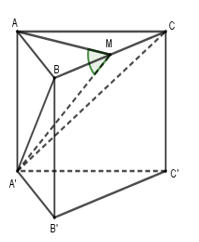
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a\), góc giữa mặt phẳng \(\left( {A'BC} \right)\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({45^0}\). Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng
- A \(\dfrac{{3{a^3}}}{8}\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
- C \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
- D \(\dfrac{{{a^3}\sqrt 3 }}{8}\)
Phương pháp giải:
- Xác định góc \({45^0}\) (góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng mà cùng vuông góc với giao tuyến).
- Tính chiều cao, diện tích đáy và suy ra thể tích theo công thức \(V = Bh\) với \(B\) là diện tích đáy, \(h\) là chiều cao.
Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(BC\) \( \Rightarrow AM \bot BC\) và \(A'M \bot BC\) (tam giác \(A'BC\) cân).
Mà \(\left( {A'BC} \right) \cap \left( {ABC} \right) = BC\) nên góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng góc giữa \(AM\) và \(A'M\) hay \(\widehat {A'MA} = {45^0}\)
Tam giác \(ABC\) đều cạnh \(a\) nên \(AM = \dfrac{{a\sqrt 3 }}{2}\).
Tam giác \(AMA'\) có \(\widehat A = {90^0},\,\,AM = \dfrac{{a\sqrt 3 }}{2}\) và \(\widehat {A'MA} = {45^0}\) nên \(AA' = AM\tan {45^0} = AM = \dfrac{{a\sqrt 3 }}{2}\).
Thể tích khối lăng trụ: \(V = {S_{ABC}}.AA' = \dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{3{a^3}}}{8}\).
Chọn A.