Câu hỏi
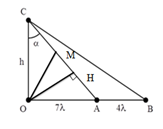
Một sóng hình sin lan truyền trên mặt nước từ nguồn O với bước sóng λ. Ba điểm A, B, C trên hai phương truyền sóng sao cho OA luôn vuông góc với OC và B là một điểm thuộc tia OA sao cho OB > OA. Biết OA = 7λ. Tại một thời điểm người ta quan sát thấy giữa A và B có 5 đỉnh sóng (kể cả A và B). Di chuyển điểm C sao cho góc ACB đạt giá trị lớn nhất thì số điểm dao động ngược pha với nguồn trên đoạn AC lúc này bằng
- A 7
- B 5
- C 6
- D 4
Phương pháp giải:
Sử dụng giản đồ vecto và kĩ năng đọc đồ thị
Áp dụng định lí hàm số sin trong tam giác và tính chất dãy tỉ số bằng nhau.
Công thức lượng giác: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\)
Áp dụng công thức lượng giác: $\tan (a - b) = \frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}$
- Bất đẳng thức Cô – si :\(a + b \ge 2\sqrt {ab} \) Dấu ‘’=’’ xảy ra khi a = b
Lời giải chi tiết:
Khi điểm M dao động ngược pha với nguồn:${{d}_{M}}=(2k+1)\frac{\lambda }{2}$
Giữa A và B có 5 đỉnh sóng với A,B cũng là đỉnh sóng:$ \Rightarrow AB = 4\lambda $
Ta có:
$\left\{ \begin{array}{l}
\tan \alpha = \frac{{OA}}{{OC}} = \frac{{7\lambda }}{h}\\
\tan \widehat {OCB} = \frac{{OB}}{{OC}} = \frac{{11\lambda }}{h}
\end{array} \right.$
$ \Rightarrow \tan \widehat {ACB} = \tan (\widehat {OCB} - \alpha ) = \frac{{\tan \widehat {OCB} - \tan \alpha }}{{1 + \tan \widehat {OCB}.\tan \alpha }} = \frac{{\frac{{4\lambda }}{h}}}{{1 + \frac{{77{\lambda ^2}}}{{{h^2}}}}} = \frac{{4\lambda }}{{h + \frac{{77{\lambda ^2}}}{h}}}$
Áp dụng bất đẳng thức Cô si: $\tan \widehat{ACB}$ lớn nhất khi $h=\frac{77{{\lambda }^{2}}}{h}\Rightarrow h=\sqrt{77}.\lambda $
Gọi M là điểm trên AC dao động ngược pha với nguồn.
${{d}_{M}}=(2k+1)\frac{\lambda }{2}$
Kẻ OH$ \bot $AC. Sử dụng hệ thức lượng trong tam giác vuông OAC :
$\begin{array}{l}
\frac{1}{{O{H^2}}} = \frac{1}{{O{C^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{77{\lambda ^2}}} + \frac{1}{{{7^2}{\lambda ^2}}} = \frac{{18}}{{539{\lambda ^2}}}\\
\Rightarrow OH = \frac{{7\sqrt {22} }}{6}\lambda
\end{array}$
Xét M trên đoạn HC:
$\begin{array}{l}
OH \le OM \le OC\\
\Rightarrow \frac{{7\sqrt {22} }}{6}\lambda \le (2k + 1)\frac{\lambda }{2} \le \sqrt {77} \lambda \\
\Rightarrow 4,97 \le k \le 8,27\\
\Rightarrow k = 5,6,7,8
\end{array}$
Có 4 giá trị k, như vậy trên đoạn HC có 4 vị trí dao động ngược pha với nguồn.
Tương tự xét M trên đoạn HA ta cũng tìm được 2 vị trí
Tổng cộng có 6 vị trí có điểm dao động ngược pha với nguồn.
Chọn C