Câu hỏi
Cho hàm số \(y = f\left( x \right)\), hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(g\left( x \right) = 2f\left( {\dfrac{{5\sin x - 1}}{2}} \right) + \dfrac{{{{\left( {5\sin x - 1} \right)}^2}}}{4} + 3\) có bao nhiêu cực trị trên khoảng \(\left( {0;2\pi } \right)\)?
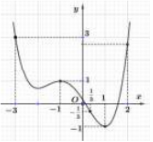
- A 9
- B 8
- C 7
- D 6
Phương pháp giải:
Đặt \(t = \dfrac{{5\sin x - 1}}{2}\).
Lời giải chi tiết:
Đặt \(t = \dfrac{{5\sin x - 1}}{2}\) ta có \(g\left( t \right) = 2f\left( t \right) + {t^2} + 3\).
Ta có: \(\forall x \in \left( {0;2\pi } \right) \Rightarrow - 1 \le \sin x \le 1 \Leftrightarrow - 5 \le 5\sin x \le 5 \Leftrightarrow - 6 \le 5\sin x - 1 \le 4 \Leftrightarrow - 3 \le \dfrac{{5\sin x - 1}}{2} \le 2\)
\( \Rightarrow - 3 \le t \le 2 \Leftrightarrow t \in \left[ { - 3;2} \right]\).
Xét hàm số \(g\left( t \right) = 2f\left( t \right) + {t^2} + 3\) trên đoạn \(\left[ { - 3;2} \right]\) ta có:
\(g'\left( t \right) = 2f'\left( t \right) + 2t = 0 \Leftrightarrow f'\left( t \right) + t = 0 \Leftrightarrow f'\left( t \right) = - t\).
Vẽ đồ thị hàm số \(y = f'\left( t \right)\) và đường thẳng \(y = - t\) trên cùng hệ trục tọa độ \(Oxy\) ta có:
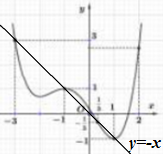
Dựa vào đồ thị hàm số ta thấy trong đoạn \(\left[ { - 3;2} \right]\) đường thẳng \(y = - t\) cắt đồ thị hàm số \(y = f'\left( t \right)\) tại 4 điểm phân biệt và qua cả 4 điểm đó \(g'\left( t \right)\) đều đổi dấu, đó là các điểm \(t \in \left\{ { - 3; - 1;0;1} \right\}\).
+) \(t = - 3 \Rightarrow \dfrac{{5\sin x - 1}}{2} = - 3 \Leftrightarrow \sin x = - 1 \Leftrightarrow x = - \dfrac{\pi }{2}\).
+) \(t = - 1 \Rightarrow \dfrac{{5\sin x - 1}}{2} = - 1 \Leftrightarrow \sin x = \dfrac{{ - 1}}{5} \Leftrightarrow \left[ \begin{array}{l}x = \arcsin \left( { - \dfrac{1}{5}} \right) + 2\pi \\x = \pi - \arcsin \left( { - \dfrac{1}{5}} \right)\end{array} \right.\)
+) \(t = 0 \Rightarrow \dfrac{{5\sin x - 1}}{2} = 0 \Leftrightarrow \sin x = \dfrac{1}{5} \Leftrightarrow \left[ \begin{array}{l}x = \arcsin \left( {\dfrac{1}{5}} \right)\\x = \pi - \arcsin \left( {\dfrac{1}{5}} \right)\end{array} \right.\)
+) \(t = 1 \Rightarrow \dfrac{{5\sin x - 1}}{2} = 1 \Leftrightarrow \sin x = \dfrac{3}{5} \Leftrightarrow \left[ \begin{array}{l}x = \arcsin \left( {\dfrac{3}{5}} \right)\\x = \pi - \arcsin \left( {\dfrac{1}{5}} \right)\end{array} \right.\)
Vậy hàm số đã cho có 7 điểm cực trị.
Chọn C







