Câu hỏi
Cho lăng trụ đều \(ABC.A'B'C'\) cạnh đáy bằng \(a\). Biết khoảng cách từ \(A\) đến \(\left( {A'BC} \right)\) bằng \(\dfrac{a}{2}\). Tính thể tích lăng trụ đã cho.
- A \(\dfrac{{\sqrt 2 {a^3}}}{{16}}\)
- B \(\dfrac{{3\sqrt 3 {a^3}}}{{16}}\)
- C \(\dfrac{{3\sqrt 2 {a^3}}}{{16}}\)
- D \(\dfrac{{\sqrt 3 {a^3}}}{{16}}\)
Phương pháp giải:
+) Dựng khoảng cách từ A đến (A’BC).
+) Tính \(AA'\). Tính \({{V}_{ABC.A'B'C'}}=AA'.{{S}_{ABC}}\).
Lời giải chi tiết:
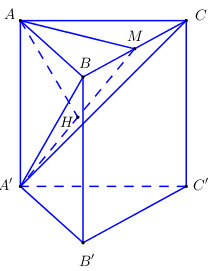
Gọi \(M\) là trung điểm của \(BC\Rightarrow AM\bot BC\).
Ta có \(\left\{ \begin{align} & BC\bot AM \\ & BC\bot AA' \\ \end{align} \right.\Rightarrow BC\bot \left( AA'M \right)\).
Trong \(\left( AA'M \right)\) kẻ \(AH\bot A'M\) ta có:
\(\left\{ \begin{align} & AH\bot A'M \\ & AH\bot BC \\ \end{align}\right.\Rightarrow AH\bot \left( A'BC \right)\Rightarrow d\left( A;\left( A'BC \right)\right)=AH=\frac{a}{2}\).
Tam giác \(ABC\) đều cạnh \(a\Rightarrow AM=\frac{a\sqrt{3}}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(AA'M\) ta có:
\(\eqalign{
& {1 \over {A{H^2}}} = {1 \over {AA{'^2}}} + {1 \over {A{M^2}}} \Leftrightarrow {4 \over {{a^2}}} = {4 \over {3{a^2}}} + {1 \over {AA{'^2}}} \cr
& \Leftrightarrow AA{'^2} = {{3{a^2}} \over 8} \Leftrightarrow AA' = {{a\sqrt 6 } \over 4} \cr} \)
Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = {{a\sqrt 6 } \over 4}.{{{a^2}\sqrt 3 } \over 4} = {{3\sqrt 2 {a^3}} \over {16}}\)
Chọn B.







