Câu hỏi
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh bằng \(a\sqrt 2 \). Gọi \(M,\,\,N,\,\,E,\,\,F,\,\,P,\,\,Q\) lần lượt là tâm của 6 mặt của hình lập phương. Tính thể tích khối đa diện \(MNEFPQ\).
- A \(\sqrt 2 {a^3}\)
- B \(2\sqrt 2 {a^3}\)
- C \(\dfrac{{\sqrt 2 }}{3}{a^3}\)
- D \(\dfrac{{2\sqrt 2 {a^3}}}{3}\)
Phương pháp giải:
Thể tích khối bát diện đều cạnh \(a\) là \(V = \dfrac{{\sqrt 2 }}{3}{a^3}\).
Lời giải chi tiết:
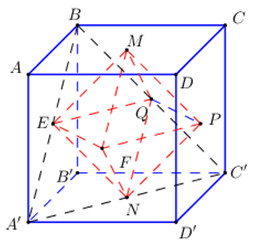
Đa diện \(MNEFPQ\) là hình bát diện đều có cạnh \(EQ = \dfrac{1}{2}A'C' = \dfrac{1}{2}.a\sqrt 2 .\sqrt 2 = a\).
Vậy \({V_{MNEFPQ}} = \dfrac{{\sqrt 2 }}{3}{a^3}\).
Chọn C.
Câu hỏi trước
