Câu hỏi
Một sợi dây đàn hồi căng ngang đang có sóng dừng ổn định. Trên dây, hai điểm M vàN nằm hai bên của nút sóng O, có khoảng cách \(MO = 2ON = \frac{\lambda }{3}\) . Hỏi tại thời điểm t, khi li độ của điểm N là uN = 8mm thì tại thời điểm \(t' = t + \frac{T}{2}\) li độ của điểm M là bao nhiêu
- A \({u_M} = 8mm\)
- B \({u_M} = 8\sqrt 3 mm\)
- C \({u_M} = - 8\sqrt 3 mm\)
- D \({u_M} = - 8mm\)
Phương pháp giải:
Phương pháp :
Ứng dụng vòng tròn lượng giác trong sóng cơ học
Lời giải chi tiết:
Cách giải :
Độ lệch pha giữa N và M là :
\(\Delta {\varphi _{NM}} = \frac{{2\pi d}}{\lambda } = \frac{{2\pi \left( {\frac{\lambda }{3} + \frac{\lambda }{6}} \right)}}{\lambda } = \pi \) → N và M dao động ngược pha nhau
Biểu diễn trên đường tròn lượng giác ta có :
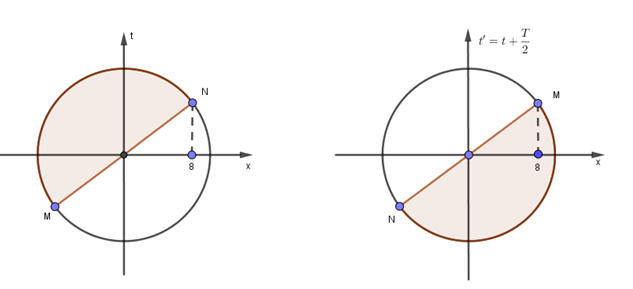
Từ vòng tròn lượng giác ta thấy tại thời điểm \(t' = t + \frac{T}{2}\) li độ của điểm M là 8 mm
Chọn A
Câu hỏi trước
