Phương pháp giải:

Biên độ dao động tại điểm cách nút dừng gần nó nhất một đoạn d là \({{A}_{C}}\text{=A}\sin \frac{2\pi d}{\lambda }\)

Độ lệch pha của một điểm trên phương truyền sóng dừng so với nguồn là \(\Delta \varphi =\frac{2\pi d}{\lambda }\)

Lời giải chi tiết:

A và B dao động ngược pha => A và B nằm ở hai bó sóng cạnh nhau

Khoảng cách gần nhất giữa AB là λ/2 = 20cm => λ = 40cm

Gọi A_b là biên độ của bụng sóng. Khoảng cách xa nhất giữa A và B là:

\(2\sqrt{{{10}^{2}}+A_{b}^{2}}=10\sqrt{5}\Rightarrow {{A}_{b}}=5cm\)

C cách A 35cm => C cách nút sóng gần nó nhất đoạn d = 5cm

Biên độ dao động tại C: \({{A}_{C}}\text{=A}\sin \frac{2\pi d}{\lambda }=2,5\sqrt{2}cm\)

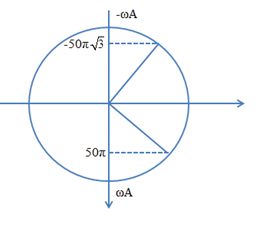
Thời điểm ban đầu v_A = 50πcm/s và thời điểm t = T/4 có v_A = \(-50\pi \sqrt{3}\)cm/s được biểu diễn như hình vẽ

Ta có: \({{\left( \frac{50\pi }{\omega A} \right)}^{2}}+{{\left( \frac{50\pi \sqrt{3}}{\omega A} \right)}^{2}}=1\Rightarrow \omega =20\pi (rad/s)\Rightarrow T=0,1s\)

Phương trình dao động của ba điểm A, B, C là :

            \({{x}_{A}}=5\cos (20\pi t-\frac{\pi }{6})cm\)

\({{x}_{B}}=5\cos (20\pi t-\frac{\pi }{6}+\pi )cm=5\cos (20\pi t+\frac{5\pi }{6})cm\)

\({{x}_{C}}=2,5\sqrt{2}\cos (20\pi t-\frac{\pi }{6}-\frac{2\pi .35}{40})cm=2,5\sqrt{2}\cos (20\pi t-\frac{23\pi }{12})cm\)

Ba điểm A, B, C thằng hàng khi

\({{x}_{B}}=\frac{{{x}_{A}}+{{x}_{C}}}{2}\Rightarrow {{x}_{A}}+{{x}_{C}}-2{{x}_{B}}=0\Rightarrow x=2,5\sqrt{2}\text{cos(20}\pi \text{t +}\frac{7\pi }{12})=0\)

Trong 1 chu kỳ x = 0 hai lần

Sau thời gian t =  1009T có 2018 lần x = 0 và đi tới vị trí ban đầu

Thời điểm x = 0 lần thứ 2019 là  1009T+ \(\frac{11}{24}T\) = 100,945s

Chọn D